АНДРОНОВА-ВИТТА ТЕОРЕМА

Расстановка ударений: АНДРО`НОВА-ВИ`ТТА ТЕОРЕ`МА

АНДРОНОВА-ВИТТА ТЕОРЕМА - модификация теоремы Ляпунова (об устойчивости периодич. решения неавтономной системы дифференциальных уравнений) для автономной системы

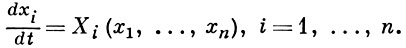
(1)

Пусть

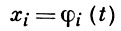
(2)

- периодич. решение системы (1) и

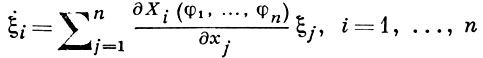
(3)

- соответствующая система уравнений в вариациях, имеющая в рассматриваемом случае всегда один нулевой характеристич. показатель. Тогда справедлива А.-В. т. : если n - 1 характеристич. показателей системы (3) имеют отрицательные действительные части, то периодич. решение (2) системы (1) устойчиво по Ляпунову (см. Ляпунова характеристический показатель, Устойчивость по Ляпунову).

А.-В. т. впервые была сформулирована А. А. Андроновым и А. А. Виттом в 1930 (см. [1], с. 45) и доказана ими же в 1933 ([1], с. 140).

Лит. : [1] Андронов А. А., Собрание трудов, М., 1956; [2] Понтрягин Л. С. Обыкновенные дифференциальные уравнения, 2 изд., М., 1965.

Е. А. Леонтович-Андронова.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.