АНАЛИТИЧЕСКОЕ ПРОСТРАНСТВО

Расстановка ударений: АНАЛИТИ`ЧЕСКОЕ ПРОСТРА`НСТВО

АНАЛИТИЧЕСКОЕ ПРОСТРАНСТВО - обобщение понятия аналитического многообразия. Локальной моделью (и одновременно важнейшим примером) аналитич. пространства над полным недискретно нормированным полем k является аналитическое множество X в области U n-мерного пространства kⁿ над полем k, заданное уравнениями f₁ =... = f_p = 0 (где f_i - аналитич. функции в U), к-рое снабжено пучком , получающимся при ограничении на X пучка _U /I, где _U - пучок ростков аналитич. функций в U, а I - подпучок идеалов, порожденный f₁, ..., f_p . Аналитическим пространством над к наз. окольцованное пространство, локально изоморфное окольцованному пространству (X, ) указанного выше вида. Если k - поле действительных чисел ℝ, говорят о вещественных аналитических пространствах; если k - поле комплексных чисел С, - о комплексных аналитических (просто комплексных) пространствах; если k - поле р-адических чисел ℚ_p, - о р-адических аналитических пространствах.

Аналитическим (голоморфным) отображением одного аналитич. пространства (X, _X) в другое (Y, _Y) наз. морфизм (X, _X) → (Y, _Y) в смысле теории окольцованных пространств, т. е. пара (φ₀, φ₁), где φ₀ : X → Y - непрерывное отображение, а φ₁ : φ₀^{- 1}_Y → _X - гомоморфизм пучков. Точка х А. п. (X, ) наз. простой (или неособой), если х обладает окрестностью, над к-рой (X, ) изоморфно пространству вида (U, _U), где U - область в kⁿ . В противном случае х наз. особой точкой. Пространство наз. гладким, если все его точки просты. Гладкое аналитич. пространство - это не что иное, как аналитич. многообразие.

Размерность dim_x X А. п. А в точке х ∈ Х определяется как размерность соответствующего аналитич. множества в локальной модели. Глобальная размерность определяется формулой

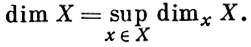
Пусть m_x - максимальный идеал в локальном кольце _x (х ∈ Х). Векторное пространство Т_x (Х) = (m_x /m²_x)* над k наз. касательным пространством к X в точке х, а Т_x (Х) = m_x /m²_x - кокасательным пространством. Число

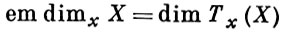
наз. касательной размерностью, или размерностью вложения, в точке х (последнее наименование связано с тем, что em dim X является наименьшим из чисел n таких, что (X, ) в окрестности точки х изоморфно локальной модели в пространстве kⁿ). Размерность dim_x *X ≤ em dim_x X, причем равенство имеет место тогда и только тогда, когда х - простая точка. Определяется также размерность

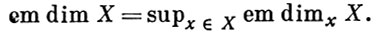
Каждое аналитич. отображение А. п. φ = (φ₀, φ₁) : (X, _X) → (Y, _Y) определяет линейное отображение dφ_x : T_x (X) → T_{φ0 (x)} (Y), к-рое наз. его дифференциалом в точке х ∈ X.

А. п. (X, ) наз. приведенным, если его локальная модель в окрестности любой точки обладает тем свойством, что I состоит из всех ростков голоморфных функций, обращающихся в 0 на X ⊂ U. В случае алгебраически замкнутого поля к это равносильно тому, что слои _x (х ∈ Х) пучка не содержат нильпотентных элементов. Всякое гладкое пространство является приведенным. Если (X, ) приведено, то можно считать, что состоит из ростков нек-рых непрерывных функций на X. Сечения пучка на приведенном пространстве (X, ) отождествляются с аналитич. функциями на А, т. е. с аналитическими отображениями X → k. Для произвольного А. п. (X, ) имеется естественный эпиморфизм пучков red : → ̃ (где (X, ̃ - приведенное А. п.), к-рый наз. приведением, или редукцией. Если f ∈ Г(X, ) - сечение пучка , то можно говорить о значении сечения f в точке х ∈ Х (оно совпадает со значением аналитич. функции red f в точке х). Поэтому алгебру Г(X, ) и в неприведенном случае часто наз. алгеброй аналитических (голоморфных) функций на (X, ). Пучки - модулей на А. п. (X, ) наз. также аналитическими пучками.

Если (X, ) - А. п., то каждое открытое U ⊂ X определяет открытое подпространство (U, |U). С другой стороны, можно ввести понятие аналитич. подпространства в (X, ), к-рое обязательно замкнуто. Множество Y ⊂ X наз. аналитическим, если в окрестности каждой точки х ∈ Х оно определяется конечным числом аналитич. уравнений. С таким множеством связан пучок идеалов I_Y ⊂ , состоящий из ростков всех аналитич. функций, равных 0 на Y. Обратно, каждый аналитический пучок идеалов конечного типа I ⊂ определяет аналитич. множество Y ⊂ X. Если _Y = |_Y |Y, получается А. п. (Y, _Y), к-рое наз. аналитическим подпространством в (X, ); имеется естественный морфизм (1, φ₁) : (Y, _Y) → (Х, ). Примером аналитич. подпространства в пространстве (X, ) является его редукция.

Понятие А. п. возникло как обобщение понятия аналитич. многообразия. Такое обобщение подсказывала прежде всего алгебраич. геометрия, в к-рой уже давно систематически рассматривались пространства с особыми точками. Влияние идей алгебраич. геометрии непосредственно отразилось на окончательной формулировке понятия А. п. (для комплексных пространств в приведенном случае она была дана в [9], в общем случае - в [6]). В частности, каждая схема конечного типа над полным нормированным полем k естественным образом определяет А. п. над k. Это соответствие схем и А. п. над k для приведенных комплексных пространств изучалось в [9], где теория А. п. была названа «аналитической геометрией». В дальнейшем обе геометрии развивались параллельно, причем обмен идеями между ними существенно способствовал успехам, достигнутым в обеих этих областях.

В теории функций многих комплексных переменных пространства с особыми точками возникли первоначально как римановы области, являющиеся аналогом римановых поверхностей функций одного переменного. Используя их в качестве локальных моделей, X. Бенке и К. Штейн (Н. Behnke, К. Stein, 1951) определили нек-рый класс окольцованных пространств, к-рый, как показано в [5], совпадает с классом приведенных нормальных аналитических пространств. Локальная геометрия аналитич. множеств в ℂⁿ была изучена еще В. Рюккертом (W. Buckert) в 1932. Наконец, негладкие А. п. естественным образом возникают в теории автоморфных функций, как факторпространства аналитич. многообразий по собственным дискретным группам автоморфизмов. р-адические аналитич. множества появились впервые в работах Т. Сколема (Т. Scolem, 1935) в связи с нек-рыми задачами теории чисел.

Теория А. п. имеет два аспекта - локальный и глобальный. Локальная аналитич. геометрия рассматривает ростки аналитич. множеств в пространстве kⁿ, снабженные пучками указанного выше вида. Основную роль здесь играет изучение свойств алгебры сходящихся степенных рядов от n переменных над k и ее факторов - так наз. аналитич. алгебр, начало к-рому положил еще К. Вейерштрасс (К. Weierstrass). К локальной теории относятся теория нормализации, изучение особых точек, локальных свойств аналитич. функций и отображений и др. Основные результаты в этой области получены в случае, когда поле к алгебраически замкнуто (см. [1], [4], [7]). Здесь появляется важное понятие когерентного аналитического пучка, играющее далее ведущую роль в глобальной теории. В частности, структурный пучок А. п. (X, ) и пучок идеалов I_Y любого аналитич. множества Y ⊂ X оказываются (в случае алгебраически замкнутого k) когерентными. Хорошо изучен также случай k = ℝ.

Глобальная аналитич. геометрия изучает свойства аналитич. функций, отображений и других аналитич. объектов, заданных «в целом» на всем А. п., а также геометрич. свойства этих пространств. В процессе изучения комплексных А. п. были выделены их естественные классы. Это прежде всего класс Штейна пространств, к-рый можно грубо охарактеризовать как класс пространств, обладающих достаточно большим запасом глобальных голоморфных функций. Пространства Штейна являются наиболее естественным многомерным обобщением областей комплексной плоскости, рассматриваемых в классич. теории функций одного комплексного переменного. Этот класс пространств по существу совпадает с классом аналитич. подпространств в пространствах ℂⁿ . Его алгебраич. аналогом является класс аффинных алгебраич. многообразий (см. Аффинное многообразие).

Для области D ⊂ ℂⁿ голоморфная полнота равносильна тому, что D - голоморфности область, т. е. что в D существует голоморфная функция, не продолжающаяся в большую область. Граница области голоморфности обладает свойством псевдовыпуклости, т. е. ведет себя по отношению к локальным аналитич. подмногообразиям в ℂⁿ так же, как выпуклая поверхность по отношению к линейным вещественным подмногообразиям. Вопрос о справедливости обратного утверждения (см. Леей проблема) породил ряд исследований и привел к новой характеризации пространств Штейна.

В известном смысле противоположным является класс компактных комплексных пространств. Справедливо следующее обобщение классич. теоремы Лиувилля: функции, голоморфные на приведенном компактном пространстве, постоянны на каждой связной компоненте этого пространства и, следовательно, составляют конечномерное векторное пространство. Обобщением этой теоремы являются конечности теоремы, утверждающие конечномерность групп когомологии со значениями в когерентном аналитич. пучке. Рассматриваются также голоморфно выпуклые комплексные пространства, q-полные, q-псевдовыпуклые, q-псевдовогнутые пространства, являющиеся обобщением пространств Штейна и компактных пространств.

Перечисленные классы комплексных пространств имеют свои аналоги в теории голоморфных отображений. Напр., компактным пространствам соответствуют собственные голоморфные отображения, голоморфно полным - штейновы отображения и т. п. Для многих теорем найдены «относительные» аналоги, причем «абсолютный» вариант теоремы получается из «относительного» в случае, когда все пространство отображается в точку. Соответствующим обобщением теорем конечности являются теоремы о когерентности прямых образов когерентных аналитич. пучков при голоморфных отображениях, первая и важнейшая из к-рых (для собственных отображений) была доказана Г. Грауэртом (см. [6]).

Большую роль в теории комплексных пространств играют голоморфные отображения специального вида - так наз. модификации, т. е. отображения f : X → Y, индуцирующие изоморфизм открытых подпространств X\X₁ → Y\Y₁, где X₁ ⊂ X, Y₁ ⊂ Y - нек-рые аналитические множества. При этом говорят, что Y получается из X путем «стягивания» подмножества X₁ на Y₁, а X из Y - путем «раздувания» подмножества Y₁ в X₁ . Особый интерес представляют аналитич. подмножества, к-рые можно стянуть в точку (исключительные аналитические множества); их характеризация дана Г. Грауэртом (см. [6]). Естественной проблемой аналитич. геометрии является следующая проблема разрешения особенностей: можно ли «раздуть» подпространство А. п. так, чтобы все пространство стало гладким? Следует отметить, что модификации в алгебраич. геометрии изучались еще в 19 в., а в аналитич. геометрии были введены X. Бенке (Н. Behnke) и К. Штейном (К. Stein) в 1951 в связи с понятием римановой области.

Другим естественным объектом изучения, также тесно связанным с идеями алгебраич. геометрии, являются мероморфные функции на комплексных пространствах и их обобщения - мероморфные отображения (примером может служить «отображение», обратное к модификации). На приведенном компактном комплексном пространстве А мероморфные функции образуют поле степени трансцендентности t(X) ≤ dim X [в гладком случае это впервые доказал К. Зигель (С. Siegel) в 1955]. Пространства X, для к-рых t(X) = dim X, образуют класс, весьма близкий к классу проективных алгебраич. многообразий (см. Алгебраическое пространство); они могут быть охарактеризованы тем, что являются модификациями гладких проективных алгебраич. многообразий. Другим близким к алгебраич. многообразиям классом А. п. являются кэлеровы многообразия. Известен ряд критериев проективности компактного комплексного пространства (см. [3], [6], [13]). Большую роль в развитии этого раздела сыграли работы по автоморфным функциям многих комплексных переменных.

Теория деформаций аналитических структур изучает задачу классификации аналитич. объектов заданного типа (напр., всех комплексных структур на заданном вещественном аналитич. многообразии, всех аналитич. подпространств в заданном комплексном пространстве и т. п.), причем цель состоит в том, чтобы ввести на множестве этих объектов «естественную» структуру комплексного пространства, а также задачу описания всех аналитич. объектов, «достаточно близких» к заданному. В первом случае говорят о проблеме глобальных модулей, а во втором - о проблеме локальных модулей. Примером проблемы глобальных модулей является задача классификации всех комплексных структур на компактной римановой поверхности (см. Модули римановой поверхности).

Основным аппаратом глобальной аналитич. геометрии являются когерентные аналитические пучки и их когомологии. Первым успехом когомологического метода явилось решение А. Картаном (Н. Cartan) аддитивной Кузена проблемы и проблемы продолжения голоморфной функции с замкнутого подмногообразия Y ⊂ X для многообразия Штейна (X, О) [8]; как выяснилось, препятствия к решению этих задач лежат в группах когомологии H¹ (X, О) и H¹ (X, I_Y) соответственно.

Результаты глобальной теории, как правило, вначале доказывались для комплексных многообразий, а затем уже обобщались на случай комплексных пространств. Возникающие при этом обобщении трудности часто требовали разработки совершенно новых методов. На комплексном многообразии когомологий локально свободного аналитич. пучка можно выразить в терминах дифференциальных форм (теорема Дольбо-Серра), что дает возможность применять для их изучения методы теории эллиптич. дифференциальных уравнений и другие аналитич. методы. В негладком случае этот путь связан с большими трудностями, и часто приходится задавать классы когомологий другими способами, напр., с помощью коцепей Чеха в подходящем покрытии. Здесь оказалась полезной техника банаховых аналитических пространств, развитая в связи с проблемами модулей.

См. также Вещественное аналитическое пространство, Жесткое аналитическое пространство.

Лит. : [1] Abhyankar S., Local analytic geometry, N. Y. - L., 1964; [2] Вǎniсǎ C., Stǎnǎsilǎ O., Metode algebrice in theoria globalǎa spatülor complexe, Bucuresti, 1974; [3] Ганнинг P., Pосси X., Аналитические функции многих комплексных переменных, пер. с англ., М., 1969; [4] Grauеrt Н., Remmert R., Analytische Stellenalgebren, В., 1971; [5] их же, «Math. Ann. », 1958, Bd 136, S. 245-318; [6] Комплексные пространства, сб. переводов, М., 1965; [7] Narasimhan R., Introduction to the theory of analytic spaces, В., 1966; [8] Расслоенные пространства и их приложения, сб. переводов, М., 1958, с. 352-62; [9] Serre J.-P., «Аnn. Inst. Fourier», 1956, t. 6, p. 1-42; [10] Фукс Б. A., Специальные главы теории аналитических функций многих комплексных переменных, 2 изд., М., 1963; [11] Xёрмандер Л., Введение в теорию функций нескольких комплексных переменных, пер. с англ., М., 1968; [12] Хирцебрух Ф., Топологические методы в алгебраической геометрии, пер. с англ., М., 1973; [13] Чжэнь Шэн-шэнь, Комплексные многообразия, пер. с англ., М., 1961.

А. Л. Онищик.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.