АНАЛИТИЧЕСКОЕ ОТОБРАЖЕНИЕ

Расстановка ударений: АНАЛИТИ`ЧЕСКОЕ ОТОБРАЖЕ`НИЕ

АНАЛИТИЧЕСКОЕ ОТОБРАЖЕНИЕ, аналитический морфизм, - морфизм аналитических пространств, рассматриваемых как окольцованные пространства. А. о. пространства (X, 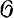_X) в пространство (Y, 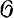_Y) есть пара (f₀, f₁), где

f₀ : X → Y

- непрерывное отображение, а

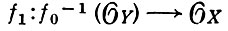
- гомоморфизм пучков колец на А. В случае комплексных пространств А. о. наз. также голоморфным отображением.

В случае, когда (X, 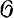_X) и (Y, 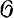_Y) - приведенные аналитич. пространства, гомоморфизм f₁ полностью определяется отображением f₀ и является обратным отображением ростков функций, отвечающим f₀ . Таким образом, в этом случае А. о. - это такое отображение f: X → Y, что для любого х ∈ А и любого φ ∈ 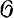_f(x) имеет место φ ○ f ∈ 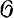_x .

Слоем А. о.

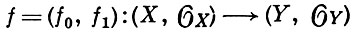
в точке y ∈ Y наз. аналитич. подпространство

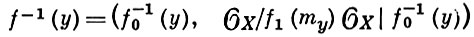
пространства (X, 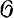_X), где m_y ∈ 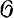_X пучок ростков функций, обращающихся в 0 в точке у. Если положить

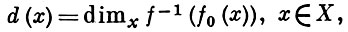
то имеет место неравенство

(*)

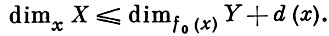
Если X и Y - приведенные комплексные пространства, то для всякого l ≥ 0 множество

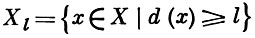
является аналитическим в А.

А. о. f = (f₀, f₁) наз. плоским в точке х ∈ X, если 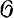_{X, x} является плоским модулем над кольцом 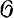_{Y, f0 (x)} . В этом случае неравенство (*) превращается в равенство. А. о. наз. плоским, если оно - плоское в каждой точке х ∈ X. Плоское А. о. комплексных пространств является открытым. Обратно, если f₀ открыто, Y гладко, а X и все слои приведены, то f - плоское А. о. Множество точек комплексного или жесткого аналитич. пространства А, у к-рых А. о. f не является плоским, будет аналитическим в А. Если X и У - приведенные комплексные пространства, причем X имеет счетную базу, то в Y существует открытое всюду плотное множество, над к-рым F - плоское А. о. Если А. о.

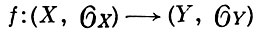
комплексных пространств плоско, то множества тех х ∈ Х, в к-рых слой f^{- 1} (x) не приведен или ненормален, являются аналитическими в 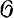(X, _X) -

Пусть F : X → Y - А. о. приведенных комплексных пространств. Если dim X < ∞, то существует стратификация

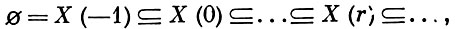
где X(r) - аналитич. множества и X(rг) = А для больших r, со следующим свойством: всякая точка х ∈ Х(r)\X(r - 1) обладает такой окрестностью U в X, что f(U ∪ X(r)) - локальное аналитич. множество в Y, все неприводимые компоненты ростка к-рого в точке f(x) имеют размерность r. В частности, если f собственное, то f(X) - аналитич. множество в X. Этот факт является частным случаем теорем конечности для А. о.

Пусть X, Y - комплексные пространства, причем X компактно. Тогда множество Моr (X, Y) всех А. о. f : X → Y можно снабдить такой структурой комплексного пространства, что отображение

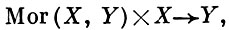
переводящее пару (f, х) в f₀ (x), аналитично. В частности, группа автоморфизмов компактного комплексного пространства X является комплексной группой Ли, аналитически действующей на X.

Лит. : [1] Remmert R., «Math. Ann. », 1956, Bd 130, S. 410-41; [2] eго же, там же, 1957, Bd 133, S. 328-70; [3] Stein К., Analytischer Abbildungen allgemeiner analytischer Räume. Colloque de topologie, Strasbourg, Avril, 1954; [4] Frisch J., «Inventiones math. », 1967, Bd 4, S. 118-38.

Д. А. Пономарев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.