АНАЛИТИЧЕСКОЕ МНОЖЕСТВО

Расстановка ударений: АНАЛИТИ`ЧЕСКОЕ МНО`ЖЕСТВО

АНАЛИТИЧЕСКОЕ МНОЖЕСТВО - подмножество полного сепарабельного метрич. пространства, являющееся непрерывным образом пространства иррациональных чисел. Понятие А. м. введено Н. Н. Лузиным [1]. Это классич. определение А. м. обобщается на случай общих метрич. и топологич. пространств.

1) А. м. в произвольном топологич. пространстве X - подмножество этого пространства, являющееся образом замкнутого подмножества пространства иррациональных чисел при полунепрерывном сверху многозначном отображении с бикомпактными образами точек и замкнутым графиком [2]. Если X - хаусдорфово, то последнее условие выполняется автоматически. Если X метризуемо, то это определение эквивалентно классическому.

2) В полном сепарабельном метрич. пространстве классич. А. м. тождественны с А-множествами. Этот факт кладется в основу второго определения А. м. (как А-множеств) в общих метрич. и топологич. пространствах (см. [3], [4], [5]). В классе вполне регулярных пространств А. м. в смысле 1) суть абсолютные А. м. в смысле 2). В классе несепарабельных метризуемых пространств используется определение 2), так как 1) дает сепарабельные А. м.

3) А. м. в хаусдорфовом пространстве (см. [6], [7]) - непрерывный образ подмножества бикомпакта типа F_{σ δ} .

4) А. м. - непрерывный образ множества, принадлежащего семейству K_{σ δ}, где K - семейство всех замкнутых бикомпактных подмножеств нек-рого топологич. пространства (см. [8]). Множество, аналитическое в смысле 3), является аналитическим в смысле 4), а это последнее является аналитическим в смысле 1).

5) В другом направлении дано обобщение в [4]: k - аналитич. множества получаются из замкнутых множеств топологич. пространства с помощью обобщенной А-операции (Бэра пространство счетного веса заменяется на пространство Бэра веса k) и являются обобщением А. м. в смысле определения 2).

Лит. : Лузин Н. Н., «С. r. Acad. sci. », 1917, v. 164, р. 91-94; [2] Frolik Z., «Mathematika», 1969, v. 16, № 2, S. 153-57; [3] Sierрinski W., General topology, Toronto, 1952; [4] Stone A., «Gen. Topol. and Appl. », 1972, v. 2, № 3, p. 249-70; [5] Куратовский К., Мостовский A., Теория множеств, пер. с англ., М., 1970; [6] Шнейдер В. Е., «Уч. зап. МГУ». 1948, в. 135, Математика, т. 2, с. 37-85; [7] Choquet G., «Ann. Inst. Fourier», 1953, t. 5, p. 131-295; [8] Sion M., «Trans. Amer. Math. Sok. », 1960, v. 96, p. 341-54.

A. Г. Елькин.

6) А. м. в теории аналитических функций - множество, определяемое локально как множество общих нулей конечного числа голоморфных функций. Если S - А. м. в открытом подмножестве U пространства n комплексных переменных Сⁿ, то это означает, что для каждой точки а ∈ U найдется окрестность V ⊂ U и конечный набор голоморфных в V функций f₁, ..., f_r таких что S ∩ V = {z ∈ V : f₁ (z) =... = f_r (z) = 0}. Если функции f_i можно выбрать (в к.-л. окрестности V) так, что ранг якобиевой матрицы (∂f_i /∂z_i1) в точке а равен r, то а наз. регулярной точкой А. м. S; число n - r наз. (комплексной) размерностью S в точке а и обозначается dim_a S. Множество S* всех регулярных точек А. м. S является открытым всюду плотным подмножеством S (в индуцированной топологии S как подмножества U). Его дополнение - множество особых точек S - есть А. м. в U, нигде не плотное на S.

По определению,

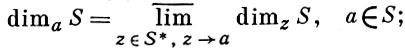
размерностью А. м. S наз. число

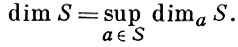
А. м. S наз. однородным k-мepным, если dim_a S = k для всех a ∈ S. Для каждого k, 0 ≤ k ≤ dimS, множество S_k = {a ∈ S : dim_a S = k} является однородным k-мерным А. м. в U\ ∪_{j > k} S_j . Таким образом, всякое А. м. в U представляется в виде конечного объединения однородных А. м. S = ∪ S_k . В особых точках dim_a (S\S*) < dim_a S, и поэтому размерность А. м. особых точек однородного k-мерного А. м. в U строго меньше k. Связные компоненты S* являются комплексными многообразиями. Так как это справедливо и для А. м. то получается разложение

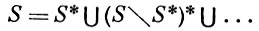
А. м. на комплексные многообразия. Более удобно разложение

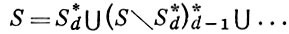
(размерности слагаемых строго убывают, d = dimS), к-рое наз. стратификацией А. м. S; связные компоненты k-го слагаемого этой суммы наз. k-мерными стратами А. м. S.

А. м. S наз. приводимым (в U), если оно является объединением к.-л. двух отличных от него А. м. в U; в противном случае S неприводимо(в U). Всякое неприводимое А. м. в U связно и однородно. А. м. S в U неприводимо тогда и только тогда, когда множество S* его регулярных точек связно. Замыкание каждой связной компоненты множества S* - неприводимое А. м. в U; такие А. м. наз. неприводимыми компонентами А. м. S. Всякое А. м. в U является локально конечным объединением своих неприводимых компонент. Если А. м. не имеют общих неприводимых компонент, то размерность их пересечения строго меньше размерности каждого из них. Если пересечение двух неприводимых А. м. в U содержит множество, открытое на каждом из них, то эти А. м. совпадают (теорема единственности).

А. м. S в U наз. неприводимым в точке a ∈ S, если существует фундаментальная система окрестностей V_i точки а в U такая, что все А. м. S ∩ V_i в V_i неприводимы; при этом а наз. точкой неприводимости A. м. S. В окрестности каждой точки неприводимости А. м. устроено как аналитическое накрытие, т. е. для каждой такой точки a ∈ S, dim_a S = k, найдутся связная окрестность V ⊂ U, линейное отображение λ : ℂⁿ → ℂ^k и А. м. τ ∈ λ (V)такие, что сужение λ на S ∩ V есть собственное отображение на λ (V), а сужение λ на (S ∩ V)\λ^{- 1} (σ) есть конечнократное локально биголоморфное накрытие над λ (V)\σ. Для неприводимых одномерных А. м. отсюда вытекает (после подходящей линейной замены координат) локальное параметрич. представление вида

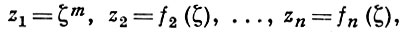
где ξ ∈ ℂ, |ξ | < r, m - целое положительное число и функции f_i голоморфны в круге |ξ | < r. Таким образом, в окрестности каждой точки неприводимости одномерное А. м. является топологич. многообразием. Для А. м. большей размерности это в общем неверно.

Объединение конечного числа и пересечение любого семейства А. м. в U суть снова А. м. в U. Всякое аналитическое в U множество замкнуто в U. Всякое компактное А. м. в U ⊂ ℂⁿ состоит из конечного числа точек. Если U связно и A. м. S ≠ U, то U\S открыто, всюду плотно в U и тоже связно. Множество всех изолированных точек А. м. S в U не имеет в U предельных точек. Более того, всякое А. м. локально связно. Связное А. м. линейно связно.

Всякое А. м. в U размерности d локально в U имеет конечную 2d-мерную меру Хаусдорфа mes_2d . Если dim_a S = k, то существуют положительные константы с и С (зависящие от а и S) такие, что

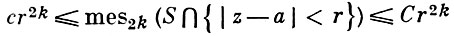
для всех достаточно малых r > 0.

Семейство А. м. инвариантно относительно биголоморфных отображений. Более того, если S - А. м. в U и f : U → U' - собственное голоморфное отображение, то f(S) - А. м. в U'.

Определение А. м. на комплексных многообразиях аналогично определению для ℂⁿ ; при этом сохраняются все перечисленные свойства, за исключением одного: в общем случае существуют компактные, но не дискретные А. м. В конкретном многообразии А. м. могут обладать нек-рыми дополнительными свойствами. Напр., в комплексном n-мерном проективном пространстве всякое А. м. является алгебраическим, т. е. совпадает с множеством общих нулей нек-рого конечного набора однородных многочленов.

Действительные А. м. в открытых подмножествах ℝⁿ определяются так же, только вместо голоморфных надо брать действительные аналитич. функции. Каждое действительное А. м. является пересечением нек-рого А. м. (в нек-ром открытом подмножестве Сⁿ) с действительным подпространством ℝⁿ ⊂ ℂⁿ .

Лит. : [1] Ганнинг Р., Росси X., Аналитические функции многих комплексных переменных, пер. с англ., М., 1969; [2] Эрве М., Функции многих комплексных переменных. Локальная теория, пер. с англ., М., 1965.

Е. М. Чирка.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.