
АНАЛИТИЧЕСКОЕ МНОГООБРАЗИЕ
Расстановка ударений: АНАЛИТИ`ЧЕСКОЕ МНОГООБРА`ЗИЕ
АНАЛИТИЧЕСКОЕ МНОГООБРАЗИЕ - многообразие с аналитич. атласом. Структура n-мерного аналитич. многообразия над полным недискретно нормированным полем к на топологич. пространстве М определяется заданием на М аналитич. атласа над k, т. е. набора карт со значениями в kn, покрывающего М, любые две карты из к-рого связаны между собой аналитически. При этом считается, что два атласа определяют одну и ту же структуру, если их объединение является аналитич. атласом. На А. м. М определен пучок 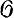 ростков k-значных аналитич. функций. Возникающий таким образом класс окольцованных пространств (М,
ростков k-значных аналитич. функций. Возникающий таким образом класс окольцованных пространств (М, 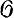 ) совпадает с классом гладких аналитич. пространств над k.
) совпадает с классом гладких аналитич. пространств над k.
В случае, если k - поле действительных чисел R, говорят о вещественных аналитических многообразиях; если k - поле комплексных чисел ℂ, - о комплексных аналитических (или просто комплексных) многообразиях; если k - поле р-адических чисел ℚp, - о р-адических аналитических многообразиях. Примерами А. м. являются: n-мерное евклидово пространство kn, n-мерное проективное пространство над k, аффинные и проективные алгебраич. многообразия над k без особых точек, группы Ли и их однородные пространства.
Понятие А. м. восходит к Б. Риману и Ф. Клейну (В. Riemann, F. Klein), но впервые было точно сформулировано Г. Вейлем в книге [4] для случая римановых поверхностей, т. е. одномерных комплексных многообразий. В настоящее время (70-е гг.) А. м. естественно рассматривать как частный случай аналитических пространств, к-рые можно грубо описать как «многообразия с особыми точками». Понятие аналитич. пространства возникло в 50-х гг. 20 в. и стало основным объектом теории аналитич. функций; многие фундаментальные результаты, полученные для А. м., удалось перенести на негладкий случай. Изложение общих свойств А. м. над произвольным полем можно найти в [3].
Существует тесная связь между теориями вещественных аналитических и дифференцируемых многообразий, а также между теориями вещественных и комплексных аналитич. многообразий. Очевидно, на всяком вещественном А. м. определена естественная структура многообразия класса С∞ . В 1936 X. Уитни (Н. Whitney) доказал, что и обратно, на всяком паракомпактном многообразии класса С∞ можно определить аналитич. структуру над ℝ, индуцирующую исходную гладкую структуру. Из теоремы Г. Грауэрта (Н. Grayert) о вложимости паракомпактного аналитич. многообразия над ℝ в евклидово пространство следует, что эта аналитич. структура определена однозначно с точностью до изоморфизма (не обязательно тождественного) (см. [2]).
На каждом комплексном многообразии М определена естественная структура вещественного А. м. (удвоенной размерности). Ответ на обратный вопрос, т. е. на вопрос о существовании и единственности комплексной структуры на заданном вещественном А. м., получен только в простейших случаях. Так, если М-связное двумерное вещественное А. м., то необходимыми и достаточными условиями существования комплексной структуры на М являются паракомпактность и ориентируемость, а задача классификации этих структур есть классич. задача о модулях римановых поверхностей. Имеется классификация компактных аналитических поверхностей (т. е. двумерных компактных комплексных многообразий), дающая частичный ответ на поставленный выше вопрос для 4-мерных вещественных многообразий. С другой стороны, при помощи топологич. методов можно указать классы вещественных многообразий, не допускающих почти комплексных и тем более комплексных структур. К таким многообразиям относятся сферы S2k при k ≠ 1, 3. Описание комплексных структур, достаточно близких к заданной, дает теория деформаций аналитических структур, важную роль в к-рой играют банаховы А. м. - бесконечномерные аналоги А. м.
Лит. : [1] Бурбаки Н., Дифференцируемые и аналитические многообразия. Сводка результатов, пер. с франц., М., 1975; [2] Нарасимхан Р., Анализ на действительных и комплексных многообразиях, пер. с англ., М., 1971; [3] Серр Ж.-П., Алгебры Ли и группы Ли, пер. с англ. и франц., М., 1969; [4] Wеуl Н., Die Idee der Riemannschen Fläche, 3 Aufl. Stuttg., 1955.
А. Л. Онищик.
Источники:
- Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'