АНАЛИТИЧЕСКИЙ ОБРАЗ

Расстановка ударений: АНАЛИТИ`ЧЕСКИЙ О`БРАЗ

АНАЛИТИЧЕСКИЙ ОБРАЗ - расширение понятия полной аналитической функции, получающееся при рассмотрении всех возможных элементов аналитич. функции в виде обобщенных степенных рядов (рядов Пюизё)

(*)

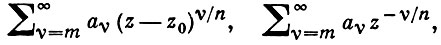
где z - комплексное переменное, m - целое, а n - натуральное числа, сходящихся соответственно в областях |z - z₀ | < r, |z| > r > 0. А. о. можно отождествить с классом всех элементов вида (*), получающихся друг из друга посредством аналитического продолжения. А. о. отличается от полной аналитич. функции присоединением всех разветвленных элементов вида (*) с n > 1, получающихся при аналитич. продолжении ее регулярных элементов с n = 1. После введения соответствующей топологии А. о. превращается в риманову поверхность данной функции.

Лит. : [1] Маркушевич А. И., Теория аналитических функций, т. 2, М., 1968, гл. 8.

Е. Д. Соломенцев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.