АНАЛИТИЧЕСКАЯ ТЕОРИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Расстановка ударений: АНАЛИТИ`ЧЕСКАЯ ТЕО`РИЯ ДИФФЕРЕНЦИА`ЛЬНЫХ УРАВНЕ`НИЙ

АНАЛИТИЧЕСКАЯ ТЕОРИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ - раздел теории обыкновенных дифференциальных уравнений, в к-ром решения исследуются с точки зрения теории аналитич. функций. Типичная постановка задачи в А. т. д. у. такова: дан нек-рый класс дифференциальных уравнений, все решения к-рых суть аналитич. функции одной переменной; требуется выяснить, какими специфич. свойствами обладают аналитич. функции, являющиеся решениями данного класса уравнений. В таком широком понимании А. т. д. у. включает теорию алгебраич. функций, теорию абелевых интегралов, теорию специальных функций и т. д. Специальные функции - Бесселя функции, Эйри функции, Лежандра функции, Лагерра функции, Эрмита функции, Чебышева многочлены, Сонина функции, Уиттекера функции, Вебера функции, Матъе функции, гипергеометрическая функция и многие другие - являются решениями линейных дифференциальных уравнений с аналитич. коэффициентами.

Линейная теория. Рассмотрим систему из n уравнений в матричной записи

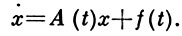
(1)

1) Пусть матрицы A (t), f(t) голоморфны в области G ⊂ C(t) (С(t) - комплексная плоскость t). Тогда всякое решение системы (1) аналитично в G (но, вообще говоря, неоднозначно, если область G неодносвязна). Предположим, что A (t) мероморфна в области G, и рассмотрим однородную систему

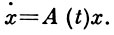
(2)

[Матрица A (t) наз. голоморфной (мероморфной) в области G, если все ее элементы голоморфны (мероморфны) в этой области.] Точка t₀ ∈ G наз. полюсом матрицы A(t) порядка ν ≥ 1, если в нек-рой окрестности этой точки

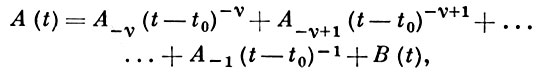
где A_{- j} - постоянные матрицы, A_{- ν} ≠ 0, а матрица В (t) голоморфна в точке t₀ . Полюс t₀ ≠ ∞ порядка ν наз. регулярной особой точкой при ν = 1 и иррегулярной особой точкой при ν ≥ 2. Случай t₀ = ∞ сводится к случаю t₀ = 0 заменой t → t^{- 1} . Ниже t₀ ≠ ∞.

2) Пусть t₀ - полюс A (t). Тогда существует фундаментальная матрица X (t) системы (2) вида

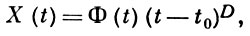
(3)

где D - постоянная матрица, Ф (t) - голоморфна при |t - t₀ | < ρ, если t₀ - регулярная особая точка, и Ф (t) голоморфна при 0 < |t - t₀ | < ρ, если t₀ - иррегулярная особая точка, для нек-рого ρ > 0. (Здесь (t - t₀)^D = = exp(ln (t - t₀)D), по определению.) Для регулярной особой точки матрица D выражается через A (t) в явном виде (см. [1], [2]); для иррегулярных особых точек это не так.

Аналогичная классификация особых точек вводится для дифференциальных уравнений порядка n с мероморфными коэффициентами. Дифференциальные уравнения и системы, все особые точки к-рых регулярны наз. дифференциальными уравнениями (системами) класса Фукса. Общий вид матрицы A (t) для такой системы:

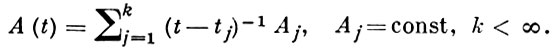
Примером дифференциального уравнения класса Фукса является гипергеометрическое уравнение.

3) Пусть A (t) = t^q B(t), q ≥ 0 - целое, В (t) голоморфна при t = ∞ (это иррегулярная особая точка, если В(∞) ≠ 0). Если S - достаточно узкий сектор вида |t| > R, α < arg t < β, то существует фундаментальная матрица вида

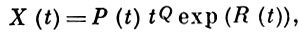
(4)

где Q - постоянная матрица, R (t) - диагональная матрица, элементы к-рой суть полиномы от t^1/p, p ≥ 1 - целое и

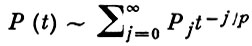
при |t| → ∞, t ∈ S. Вся плоскость C(t) разбивается на конечное число секторов, в каждом из к-рых есть фундаментальная матрица вида (4) (см. [3], [4], а также [11. [2]).

4) При аналитич. продолжении вдоль замкнутого пути γ фундаментальная матрица X(t) умножается на В_γ : X(t) - >Х(t)B_γ, где B_γ - постоянная матрица; возникает монодромии группа дифференциального уравнения. И. А. Лаппо-Данилевским [5] была исследована проблема Римана: пусть A(t) - рациональная функция от t, и пусть известны особенности фундаментальной матрицы X(t); требуется найти A(t).

5) Пусть функция z = φ (t) конформно отображает верхнюю полуплоскость Im t > 0 на внутренность многоугольника, граница к-рого состоит из конечного числа отрезков прямых и дуг окружностей. Тогда функция φ (t) удовлетворяет уравнению Шварца

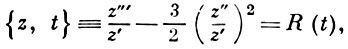
(5)

где R(t) - рациональная функция, причем уравнение 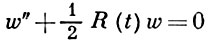(6)

принадлежит классу Фукса. Любое решение уравнения (5) может быть представлено в виде z = w₁ /w₂, где w₁, w₂ - линейно независимые решения уравнения (6). Пусть G - бесконечная дискретная группа, φ (t) - автоморфная функция группы G; тогда φ (t) может быть представлена в виде φ = w₁ /w₂, где w₁, w₂ - линейно независимые решения уравнения (6) и R(t) - нек-рая алгебраическая функция.

Нелинейная теория. 1) Рассмотрим задачу Коши:

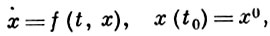
(7)

здесь t ∈ C(t), x = (x₁, ..., x_n) ∈ Сⁿ (х), f = (f₁, ..., f_n).

Теорема Коши: пусть функция f(t, х) голоморфна по (t, х) в области G ⊂ C(t) × Сⁿ (х) и точка (t₀, x⁰) ∈ G. Тогда существует δ > 0 такое, что в области |t - t₀ | < δ существует решение x(t; t₀, х⁰) задачи Коши (7), единственное и голоморфное.

Аналитич. продолжение решения x(t; t₀, х⁰) также будет решением системы (7), однако полученная в результате продолжения функция может иметь особенности и, вообще говоря, будет неоднозначной функцией от t. Возникают вопросы: какие особенности может иметь эта функция, как устроено решение в целом? В линейном случае получены окончательные ответы на эти вопросы. В нелинейном случае ситуация значительно сложнее и не выяснена достаточно полно даже в том случае, когда f_j (t, х) - рациональные функции от t, х.

2) Рассмотрим одно дифференциальное уравнение

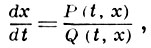
(8)

где t ∈ C, x ∈ C, a P и Q - голоморфные пo (t, x) функции в нек-рой области G. Точка (t₀, х₀) ∈ G наз. (существенно) особой точкой уравнения (8), если Р (t₀, х₀) = 0, Q (t₀, х₀) = 0. Выясним структуру решений в окрестности особой точки уравнения. Разложим Р и Q в ряды Тейлора:

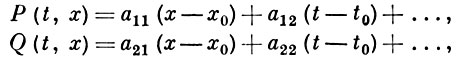
и пусть λ₁, λ₂ - собственные значения матрицы ||а_ij ||. Имеет место теорема: пусть λ_j ≠ 0 и ни одно из чисел λ₁ /λ₂, λ₂ /λ₁ не является: а) целым неотрицательным числом, б) действительным отрицательным числом. Тогда существуют окрестность U точки (t₀, х₀), окрестность V точки t̃ = 0, х̃ = 0 и функции t̃ = t̃ (t, х), x̃ = x̃ (t, х) такие, что: отображение U → V, задаваемое этими функциями, является биголоморфным; дифференциальное уравнение (8) в новых переменных принимает вид (см. [6]):

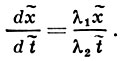
Все решения уравнения (8) в новых переменных записываются в виде x̃ = Ct̃^{λ₁ /λ₂} и х̃ ≡ 0. Таким образом, особая точка уравнения является точкой ветвления бесконечного порядка для всех решений уравнения (8) (кроме тривиальных). Особые точки решения, совпадающие с особыми точками уравнения, наз. неподвижными. В отличие от линейного случая, решение нелинейного уравнения может иметь особые точки не только в особых точках уравнения; такие особые точки решения наз. подвижными. Справедлива теорема Пенлеве: решения уравнения

Р (t, х, 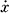) = 0,

где Р - многочлен от х и 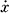с голоморфными по t коэффициентами, не имеют подвижных трансцендентных особых точек (см. [7]).

Если в уравнении (8) Р и Q суть многочлены от t, х, то в силу теоремы Пенлеве все подвижные особые точки являются алгебраическими. При замене t = 1/t', х = х'/t', уравнение (8) примет вид

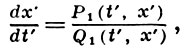
где Р₁, Q₁ - многочлены. Пусть x_j - корни уравнения Р₁ (0, х') = 0. Точки (0, х'_j) наз. бесконечно удаленными особыми точками уравнения (8); структуру решений в окрестности этих точек описывает приведенная выше теорема [6].

Пусть Р, Q - многочлены степени n. Поскольку Р, Q определяются своими коэффициентами и пара (λ Р, λ Q) задает то же уравнение, получают взаимно однозначное соответствие между уравнениями (8) и точками комплексного проективного пространства ℂ P^N (N = (n + 1) × (n + 2) - 1). Имеет место теорема: если удалить из ℂ P^N нек-рое множество меры нуль, то оставшиеся уравнения (8) обладают следующим свойством: все решения x = x(t) всюду плотны в С² = С(t) × C(х) (см. [8]).

3) Рассмотрим автономную систему

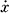= f(х), (9)

t ∈ C(t), х ∈ Сⁿ (х), f = (f₁, ..., f_n). Точка х⁰ наз. особой точкой системы (9), если f(х⁰) = 0. Справедлива теорема Пуанкаре. Пусть х⁰ - особая точка автономной системы (9). Пусть, кроме того: а) элементарные делители матрицы Якоби f'(x⁰) простые и б) собственные значения λ_j этой матрицы лежат по одну сторону от нек-рой прямой в С(λ), проходящей через начало координат. Тогда существуют окрестности U, V точек х = х⁰, х̃ = 0 и биголоморфное отображение х = х(х̃): V → V такое, что в переменных х̃ автономная система (9) имеет вид (см. [9]):

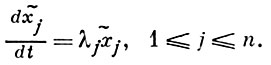
В том случае, когда выполнено только условие а), можно с помощью преобразования х = φ (х̃), где φ (х̃) - формальный степенной ряд, привести систему (9) в окрестности особой точки к системе, к-рая интегрируется в квадратурах (см. [9], [10]). Однако сходимость этих рядов доказана при предположениях, близких к а), б). В случае, когда функция f(x) и преобразование х = φ (х̃) вещественны при вещественных х, х̃, доказана теорема (см. [11]), аналогичная теореме Пуанкаре. Структура решений автономной системы (9) в целом, где f_j (x) - полиномы и n ≥ 3 к 70-м гг. 20 в. не исследована.

Лит. : [1] Коддингтон Э. А., Левинсон Н., Теория обыкновенных дифференциальных уравнений, пер. с англ., М., 1958; [2] Вазов В., Асимптотические разложения решений обыкновенных дифференциальных уравнений, пер. с англ., М., 1968; [3] Вirkhоff G. D., «Trans. Amer. Math. Soc. », 1909, v. 10, p. 436-70; [4] Trjitzïnsку W. J., «Acta math. », 1933, Bd 62, S. 167-226; [5] Лаппо-Данилeвский И. А., Применение функций от матриц к теории линейных систем обыкновенных дифференциальных уравнений, [пер. с франц. 1, М., 1957; [6] Bieberbach L., Theorie der gewöhnlichen Differentialgleichungen auf Funktionentheoretischer Grundlage dargestellt, В., 1953; [7] Голубев В. В., Лекции по аналитической теории дифференциальных уравнений, 2 изд., М. - Л., 1950; [8] Xудай-Веренов М. Г., «Матем. сб. », 1962, т. 56, № 3, с. 301-8; [9] Немыцкий В. В., Степанов В. В., Качественная теория дифференциальных уравнений, 2 изд., М. - Л., 1949; [10] Брюно А. Д., «Докл. АН СССР», 1964, т. 157, № 6, с. 1276-79; [11] 3игель К. Л., «Математика», 1961, т. 5, № 2, с. 119-28; [12] Пуанкаре А., Избранные труды, пер. с франц., т. 3, М., 1974: [13] Форд Л. Р., Автоморфные функции, пер. с англ., М., 1936.

М. В. Федорюк.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.