АМАЛЬГАМА

Расстановка ударений: АМАЛЬГА`МА

АМАЛЬГАМА - множество М, представнмое в виде теоретико-множественного объединения семейства алгебраических систем А_i из заданного класса 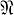с пересечениями U_ij причем для всех i, j пересечение

A_i ∩ A_j = U_ij = U_ji

непусто и является подсистемой в каждой из систем А_i, A_j . Если существует система В в классе 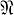, содержащая все A_i (i ∈) в качестве подсистем, то говорят, что А. М вложима в 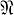-систему.

А. двух групп и вообще любая А. групп {A_i | i ∈ I}, у к-рой все пересечения U_ij (i ≠ j) совпадают между собой и равны U, всегда вкладывается в группу, напр. в свободное произведение групп A_i (i ∈ I) с объединенной подгруппой U. Существуют, однако, А. групп, не вложимые в группу. (Условия вложимости А. групп в группу см. в [1], А. полугрупп в полугруппу см. в [2].) См. также Амальгама групп.

Пусть 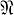- класс всех алгебр над данным полем F или класс коммутативных, антикоммутатпвных или лиевых алгебр над полем F. A. {A_i |i ∈ I} 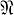- алгебр A_i с совпадающими пересечениями U_ij = U (для всех i ≠ j) вложима в 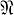- свободное произведение этих алгебр с объединенной подалгеброй U (см. [3]). Доказано (см. [4]), что A. {T_i | i ∈ I} ассоциативных тел T_i с совпадающими пересечениями Т_ij = Т(i ≠ j) вложима в ассоциативное тело.

Лит. : [1] Курош А. Г., Теория групп, 3 изд., М., 1967, с. 462; [2] Клиффорд А., Престон Г., Алгебраическая теория полугрупп, т. 2, пер. с англ., М., 1972; [3] Ширшов А. И., «Сиб. матем. ж. », 1962 т. 3, № 2, с. 297-301; [4] Соhn Р. М., «Рrос. London Math. Soc. », 1971, v. 23, № 2, p. 193-213.

Л. А. Бокуть, Д. M. Смирнов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.