АЛЬТЕРНИОН

Расстановка ударений: АЛЬТЕРНИО`Н

АЛЬТЕРНИОН - гиперкомплексное число, А. могут рассматриваться как обобщение комплексных чисел, двойных чисел (см. Двойные и дуальные числа) и кватернионов. Алгеброй ^l А_n альтернионов n-го порядка индекса l наз. алгебра ранга 2^{n - 1} над полем действительных чисел с единицей 1 и системой образующих l₁, ..., l_{n - 1}, умножение к-рых производится по формулам

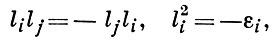
где ε_i = ±1, причем - 1 встречается l раз, а + 1, соответственно, n - l - 1 раз. Базис алгебры можно составить из элементов вида

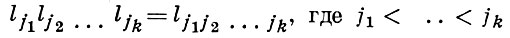
и единицы. Произвольный А. α будет иметь в этой базе запись

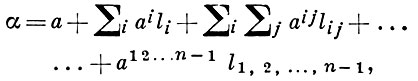
где a, aⁱ, a^ij, ..., a^{12...(n - 1)} - действительные числа. Сопряженный к А. α А. ᾱ определяется формулой

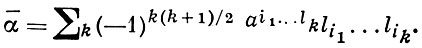
Справедливы равенства

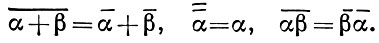
Произведение ᾱ α всегда является положительным действительным числом, величина 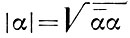наз. модулем А. α. Если принять за расстояние между А. α и #946; число |#946; - α |, то алгебры ⁰ А_n и ^l А_n (l > 0) оказываются изометричными евклидовым пространствам R_{2^{n - 1}} и псевдоевклидовым пространствам ^l R_{2^{n - 1}} соответственно. Алгебра ⁰ А₁ изоморфна полю действительных чисел, алгебра ⁰ А₂ изоморфна полю комплексных чисел, алгебра ¹ А₂ изоморфна алгебре двойных чисел, алгебра ⁰ А₃ изоморфна телу кватернионов, алгебры ¹ А₃ и ² А₃ изоморфны так наз. алгебрам антикватернионов. Элементы алгебр ⁰ А_n наз. числами Клиффорда. Алгебра ⁴ А₅ рассматривалась П. Дираком (P. Dirас) при изучении спина электрона.

Алгебра А. является частным случаем Клиффорда алгебр.

Лит. : [1] Розенфельд Б. А., Неевклидовы геометрии, М., 1955.

Н. Н. Вильямс.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.