АЛЬТЕРНАНСА ТОЧКИ

Расстановка ударений: АЛЬТЕРНА`НСА ТО`ЧКИ

АЛЬТЕРНАНСА ТОЧКИ - последовательность точек 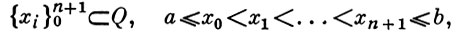в к-рых разность α_i = f(x_i) - Р_n (х_i), где f(x) - непрерывная на замкнутом множестве Q ⊂ [a, b] функция и Р_n (х) - алгебраич. многочлен степени не выше n, принимает неравные нулю значения чередующихся знаков. Аналогично вводится понятие А. т. для многочленов по чебышевской системе функций {s_k (x)}ⁿ₀ (удовлетворяющих Хаара условию). Если при этом все α_i по абсолютной величине равны

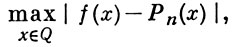
то точки {x_i}₀^{n + 1} наз. точками чебышевского альтернанса. А. т. играют важную роль в теории приближения функций. Так, в терминах А. т. формулируется Балле Пуссена теорема (об альтернансе) и критерий Чебышева (см. Чебышевский альтернанс). А. т. используются при построении многочленов наилучшего приближения.

Ю. Н. Субботин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.