АЛЬБАНЕЗЕ МНОГООБРАЗИЕ

Расстановка ударений: АЛЬБАНЕ`ЗЕ МНОГООБРА`ЗИЕ

АЛЬБАНЕЗЕ МНОГООБРАЗИЕ - абелево многообразие Alb (X), канонически сопоставляемое каждому алгебраич. многообразию X и являющееся решением следующей универсальной задачи: существует морфизм φ : X → Аlb(X) такой, что любой морфизм f: X → А в абелево многообразие А разлагается в произведение f = f' ⋅ φ, где f': A → Аlb(X) (название в честь Альбанезе; Albanese). Если X полное неособое многообразие над полем комплексных чисел, то А. м. можно описать следующим образом. Пусть Ω¹ - пространство всюду регулярных дифференциальных форм степени 1 на X. Каждый одномерный цикл γ топологич. пространства X определяет линейную функцию ω → ∫_γ ω на Ω¹ . Образ получающегося отображения Н¹ (Х, ℤ) → (Ω¹)* является решеткой Г в (Ω¹)*, а фактор-пространство (Ω¹)*/Г совпадает с А. м. многообразия А. С алгебраич. точки зрения А. м. можно рассматривать как способ задания алгебраич. структуры на нек-рой факторгруппе группы Z нульмерных циклов степени 0 на многообразии X. В случае, когда X - неособая полная кривая, Alb (X) совпадает с Якоби многообразием кривой X. Если основное поле k имеет нулевую характеристику, то имеют место равенства dim Alb (X) = dim_k H⁰ (X, Ω¹_X) = = dim_k H¹ (X, О_X). Число dim Alb (X) наз. иррегулярностью многообразия X. В случае, когда поле имеет конечную характеристику, имеет место неравенство

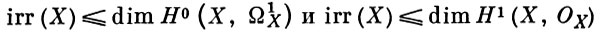
и

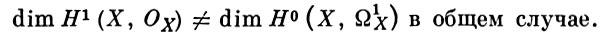
А. м. двойственно Пикара многообразию.

Лит. : [1] Бальдассарри М., Алгебраические многообразия, пер. с англ., М., 1961; [2] Lang S., Abelian varieties, N. Y. - L., 1959.

А. Н. Паршин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.