АЛЕФЫ

Расстановка ударений: А`ЛЕФЫ

АЛЕФЫ, 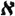, - первая буква древнееврейского алфавита, - символы, введенные Г. Кантором (G. Cantor) для обозначения кардинальных чисел (мощностей) бесконечных вполне упорядоченных множеств. Каждое кардинальное число есть нек-рый А. (следствие выбора аксиомы). Но многие теоремы об А. доказываются без аксиомы выбора. Для каждого порядкового числа α через 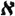_α = w{ω_α) обозначается мощность множества всех порядковых чисел, меньших ω_α . В частности, 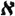₀ есть мощность множества всех натуральных чисел, 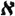₁ - мощность множества всех счетных порядковых чисел и т. д. 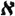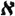Если α < β, то _α < _β - Кардинал 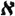_{α + 1} является наименьшим кардинальным числом, следующим за 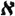_α . Обобщенная континуум-гипотеза заключается в том, что 2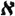^_α = 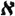_{α + 1} для любого порядкового числа α. При α = 0 равенство приобретает вид 2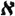^₀ = 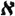₁ и составляет содержание континуум-гипотезы. Множество всех А., меньших 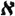_α, вполне упорядочено по величине и порядковый тип его равен α. Естественным образом определяются сумма, произведение и степень А. При этом

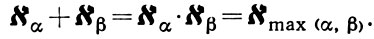
Наиболее часто встречаются следующие формулы. Рекурсивная формула Хаусдорфа:

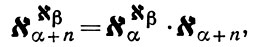
ее частным случаем при α = 0 является формула Бернштейна:

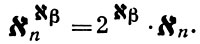
Рекурсивная формула Тарского: если порядковое число α предельно и β < cf(α), то

При этом сf(α) обозначает конфинальный характер порядкового числа α. Как и в случае кардинальных чисел, различают сингулярные А., регулярные А., предельные А., слабо недостижимые А., сильно недостижимые А. и др. Напр., 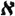_α сингулярно, если α предельно и cf(α) < α. Среди А. нет наибольшего. Множество всех А., как показал Г. Кантор, не мыслимо, т. е. такого множества не существует. См. также Вполне упорядоченное множество, Кардинальное число, Континуум-гипотеза, Множеств теория, Порядковое число.

Лит. : [1] Александров П. С., Введение в общую теорию множеств и функций, М. - Л., 1948; [2] Xаусдорф Ф., Теория множеств, пер. с нем., М. - Л., 1937; [3] Коэн П. Дж., Теория множеств и континуум-гипотеза, пер. с англ., М., 1969; [4] Куратовский К., Мостовский А., Теория множеств, пер. с англ., М., 1970.

Б. А. Ефимов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.