АЛЕКСАНДЕРА ИНВАРИАНТЫ

Расстановка ударений: АЛЕКСА`НДЕРА ИНВАРИ`АНТЫ

АЛЕКСАНДЕРА ИНВАРИАНТЫ - инварианты, связанные с модульной структурой одномерных гомологии многообразия М̃, на к-ром свободно действует свободная абелева группа J^a ранга а с фиксированной системой образующих t₁, ..., t_a .

Проекция многообразия М̃ на пространство орбит М является накрытием, отвечающим ядру К_a гомоморфизма γ : G → J_a фундаментальной группы π₁ (M) = G многообразия М. Так как К_a = π₁ (M̃), то группа В_a = К_a /К'_a, где К'_a - коммутант ядра К_a, изоморфна одномерной группе гомологии Н₁ (М̃, Z). При этом расширение 1 → K_a → G → J^a → 1 порождает расширение (*): 1 → B_a → G/K'_a → J^a → 1, к-рое определяет на В_a модульную структуру над целочисленным групповым кольцом Z(J^a) группы J^a (см. Групповая алгебра). Та же самая структура индуцируется в В_a данным действием J^a на М̃. Фиксация образующих t_i в J^a отождествляет Z(J^a) с кольцом L_a = L_a (t₁, ..., t_a) = Z[t₁, t₁^{- 1}, ..., t_a, t_a^{- 1} ] лорановых многочленов от переменных t_i . Расширение (*) чисто алгебраически определяет и определено модульным расширением (**): 0 → В_a → А_a → I_a → 0 (см. [5]). Здесь I_a - ядро гомоморфизма ε : L_a → Z, (ε t_i = 1). Модуль А_a наз. модулем Александера накрытия М̃ → М. В случае (рассмотренном впервые Дж. Александером [1]), в к-ром М = М(k) - дополнительное пространство нек-рого зацепления k кратности μ в трехмерной сфере S³, а накрытие отвечает гомоморфизму коммутирования γ_μ : G(k) → J^μ группы зацепления, - А_μ наз. модулем Александера зацепления k. Основные свойства G, существенные для дальнейшего: G/G' - свободная абелева группа, дефект группы G равен 1, G имеет копредставление {x₁, ..., x_{m + 1} ; r₁, ..., r_m}, для к-рого γ_μ (x_i) = t_i, 1 ≤ i ≤ μ, γ_μ (x_i) = 1, i > μ (см. Узлов и зацеплений диаграммы). В случае зацеплений образующие t_i ∈ J^μ отвечают меридианам компонент k_i ⊂ k и фиксируются ориентацией этих компонент и сферы.

Обычно М есть дополнительное пространство М(k) зацепления k, состоящего из μ (n - 2)-мерных сфер k_i в Sⁿ . Кроме гомоморфизма 947;_m рассматривается гомоморфизм 947;_σ : G(k) → J, где 947; (х) равно сумме коэффициентов зацепления петли, представляющей х, со всеми k_i .

Матрица 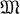_a модульных соотношений модуля А_a наз. матрицей Александера накрытия, а в случае зацеплений - матрицей Александера зацепления. Она может быть получена как матрица

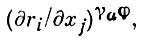
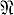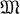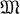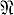где {x_i ; r_i} - копредставление группы G. При μ = 1 матрица _a модульных соотношений для В_a получается из _a отбрасыванием столбца из нулей. Матрицы _a и _a определены модулями А_a и В_a лишь с точностью до преобразований, отвечающих переходам к другим копредставлениям модуля. Однако с их помощью вычисляется ряд инвариантов модуля. Идеалами Александера наз. идеалы модуля А_a, т. е. ряд идеалов E_i (A_a) кольца L_a : (0) ⊆ E₀ ⊆... ⊆ E_{i - 1} ⊆ E_i ⊆... ⊆ (1), где E_i порождается минорами матрицы 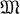_a порядка (m - k) × (m - k) и E_a = Lⁱ_a для r - i < 1. Употребляется и противоположный порядок нумерации. Так как L_a - гауссово кольцо и нётерово кольцо, то каждый идеал E_i лежит в минимальном главном идеале (Δ_i); его образующая Δ_i определена с точностью до делителей единицы t^k_i . Лоранов многочлен Δ_i (t₁, ..., t_μ) наз. i-м многочленом Александера, a Δ₁ (t₁, ..., t_μ) - просто многочленом Александера зацепления k (или накрытия M̃ → М). Если Δ_i ≠ 0, то он домножается на t₁^k₁, ..., t_μ^k_μ так, чтобы Δ_i (0, ..., 0) ≠ 0 и ≠ ∞. Гомоморфизму отвечает модуль А, идеалы E_i и полиномы Δ_i, к-рые наз., соответственно, приведенным модулем Александера, приведенными идеалами Александера и приведенными многочленами Александера зацепления k (или накрытия M̃_σ → М). Если μ = 1, то А = А¯. 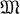(А¯) получается из заменой всех t_i на t. При μ ≥ 2 Δ¯₁ делится на (t - 1)^{μ - 2} . Полином ∇ (t) = Δ₁ (t)/(t - 1)^{μ - 2} наз. полиномом Хосокавы [4]. Модульные свойства А (k) изучены в [4], [8], [10]. Случай зацеплений исследован мало. Для μ = 1 группа H₁ (М̃ ; R) конечно порождена над любым кольцом R, содержащим Z, в к-ром Δ (0) обратим [7], в частности, над полем рациональных чисел, а если Δ (0) = + 1, то над Z. В этом случае Δ (t) - характеристич. многочлен преобразования t: H₁ (М̃ ; R) → H₁ (М̃ ; R). Степень Δ₁ (t) равна рангу H₁ (М̃ ; R); в частности, Δ₁ (t) = 1 в том и только том случае, когда H₁ (М̃ ; Z) = 0. При n = 3 идеалы зацепления обладают следующим свойством симметрии: E_i = E¯_i, где черта означает взятие образа при автоморфизме, порожденном заменой всех t_i на t_i^{- 1} . Отсюда вытекает, что Δ_i (t₁^{- 1}, ..., t_μ^{- 1}) = t₁^N₁, ..., t_μ^N_μ Δ_i (t₁, ..., t_μ) для нек-рых целых N_i . Эта симметрия является следствием двойственности Фокса-Троттера для групп узлов и зацеплений. Она может быть выведена также из Пуанкаре двойственности для многообразия М̃ с учетом свободного действия J^a (см. [3]). Если Δ_i (t₁, ..., t_μ) ≠ 0, то над полем дробей Р_μ кольца L_μ цепной комплекс С_* (М̃) ацикличен (n = 3). Следовательно, определено Рейдемейстера кручение τ ∈ Р_μ /П, отвечающее вложению L_μ ⊂ P_μ, где П - группа единиц L_μ . Для μ = 2 τ = Δ₁, для μ = 1 τ = Δ₁ /t - 1 (с точностью до единиц L_μ). Симметрия Δ₁ для n = 3 является следствием симметрии τ. В случае μ = 1 из симметрии Δ_i (t) и свойства Δ_i (1) = ±1 вытекает четность степени Δ_i (t). Степень ∇ (t) также четна [4]. Свойства многочленов узлов Δ_i (t): Δ_i (1) = ±1, Δ_i (t) = t^2k Δ_i (t^{- 1}), Δ_{i + 1} делит Δ_i и Δ_i = 1 для i, превосходящих нек-рое N, являются характеристическими, т. е. для каждого набора Δ_i (t) с этими свойствами существует узел k, для к-рого они служат многочленами Александера. Полиномы Хосокавы [4] характеризуются свойством ∇ (t) = t^2k ∇ (t^{- 1}) при любом μ ≥ 2; полиномы Δ₁ двумерных узлов - свойством Δ₁ (1) = 1.

А. и., в первую очередь многочлены, являются мощным средством различения узлов и зацеплений. Напр., среди узлов из таблицы с менее чем девятью двойными точками Δ₁ не различает только три пары (см. Узлов таблица). См. также Узлов теория, Альтернирующие узлы и зацепления.

Лит. : [1] Alexander J. W., «Trans. Amer. Math. Soc. », 1928, v. 30, № 2, p. 275-306; [2] Reidemeister K., Knotentheorie, В., 1932; [3] Blanchfield R. C., «Ann. Math. », 1957, v. 65, p. 340-56; [4] Hоsоkawa F., «Osaka J. Math. », 1958, v. 10, p. 273-82; [5] Crowell R. H., «Nagoya Math. J. », 1961, v. 19, p. 27-40; [6] Кpоуэлл P., Фокс Р., Введение в теорию узлов, пер. с англ., М., 1967; [7] Neuwirth L., Knot group, Princeton (N. Y.), 1965; [8] Crowell R. H., «J. Math. and Mech. », 1965, v. 14, № 2, p. 289-98; [9] Levine J., «Amer. J. Math. », 1967, v. 89, p. 69-84; [10] Milnоr J. W., в кн. : Conference on the topology of manifolds, v. 13, Boston (a. o.), 1968, p. 115-33.

А. В. Чернавский.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.