АЛГОРИТМОВ ТЕОРИЯ

Расстановка ударений: АЛГОРИ`ТМОВ ТЕО`РИЯ

АЛГОРИТМОВ ТЕОРИЯ - раздел математики, изучающий общие свойства алгоритмов. Содержательные явления, приведшие к образованию понятия «алгоритм», прослеживаются в математике в течение всего времени ее существования. Однако само это понятие сформировалось лишь в 20 в. и стало предметом самостоятельного изучения (по-видимому, впервые, хотя еще в расплывчатом виде) в 20-х гг. 20 в. в трудах представителей интуиционизма Л. Э. Я. Брауэра (L. Е. J. Brouwer) и Г. Вейля (Н. Weyl, см. [1]). Началом систематич. разработки А. т. можно считать 1936, когда А. Чёрч (A. Church, [2]) опубликовал первое уточнение понятия вычислимой функции (предложив отождествлять понятие всюду определенной вычислимой функции, имеющей натуральные аргументы и значения, с понятием общерекурсивной функции) и привел первый пример функции, не являющейся вычислимой, а А. М. Тьюринг (А. М. Turing, [3], [4]) и Э. Л. Пост (Е. L. Post, [5]) дали первые уточнения понятия алгоритма (в терминах идеализированных вычислительных машин, см. Тьюринга машина). В дальнейшем А. т. получила развитие в трудах С. К. Клини (S. С. Kleene), Э. Л. Поста (см. [6]-[8]), А. А. Маркова (см. [9]-[11]) и др. В частности, А. А. Марков предложил уточнять понятие алгоритма с помощью введенного им понятия нормального алгорифма (см. [10]). Наиболее общий подход к уточнению понятия алгоритма предложил А. Н. Колмогоров (см. [12], [13]).

Поскольку алгоритмы могут иметь дело лишь с так наз. конструктивными объектами, то, чтобы перенести понятия и методы А. т. на случай неконструктивных объектов, надо эти последние объекты обозначить, или поименовать, конструктивными объектами. Изучение общих свойств таких поименований (прежде всего, когда в качестве обозначений, или имен, выступают натуральные числа) составляет предмет теории нумерации (см. [14]), образующей важный раздел А. т.

Основные понятия теории алгоритмов. Областью применимости алгоритма наз. совокупность тех объектов, к к-рым он применим. Про алгоритм 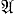говорят, что он: 1) «вычисляет функцию f», коль скоро его область применимости совпадает с областью определения f, и 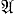перерабатывает всякий х из своей области применимости в f(х); 2) «разрешает множество А относительно множества X», коль скоро он применим ко всякому х из X и перерабатывает всякий х из X ∩ A в слово «да», а всякий х из Х\А в слово «нет»; 3) «перечисляет множество В», коль скоро его область применимости есть натуральный ряд, а совокупность результатов есть В. Функция наз. вычислимой, если существует вычисляющий ее алгоритм. Множество наз. разрешимым относительно X, если существует разрешающий его относительно X алгоритм. Множество наз. перечислимым, если либо оно пусто, либо существует перечисляющий его алгоритм.

Детальный анализ понятия «алгоритм» обнаруживает, что: (I) область возможных исходных данных и область применимости любого алгоритма суть перечислимые множества. В свою очередь, (II) для любой пары вложенных одно в другое перечислимых множеств можно подобрать алгоритм, у к-рого большее множество служит областью возможных исходных данных, а меньшее - областью применимости. Имеют место следующие основные теоремы: (III) функция f вычислима тогда и только тогда, когда перечислим ее график, т. е. множество всех пар вида < х, f(x) >. (IV) Подмножество А перечислимого множества X тогда и только тогда разрешимо относительно X, когда А и Х\А перечислимы. (V) Если А и В перечислимы, тo A ∩ B и A ∪ B также перечислимы. (VI) В каждом бесконечном перечислимом множестве X существует перечислимое подмножество с неперечислимым дополнением [в силу (IV) это перечислимое подмножество будет неразрешимым относительно А]. (VII) Для каждого бесконечного перечислимого множества X существует вычислимая функция, определенная на подмножестве этого множества и не продолжаемая до вычислимой функции, определенной на всем X. Утверждения (VI) и (II) в совокупности дают упоминаемый в статье Алгоритм пример алгоритма с неразрешимой областью применимости. Разрешимые и перечислимые множества составляют простейшие (и наиболее важные) примеры множеств, строение к-рых задается с помощью тех или иных алгоритмич. процедур. Систематич. изучение множеств конструктивных объектов с точки зрения таких свойств этих множеств, к-рые связаны с наличием тех или иных алгоритмов, образует так наз. алгоритмическую теорию множеств; нек-рые понятия, методы и результаты этой теории находят глубокие аналогии в дескриптивной теории множеств.

Алгоритмические проблемы. Проблема построения алгоритма, обладающего теми или иными свойствами, наз. алгоритмической проблемой (а. п.). Как правило,

свойство искомого алгоритма формулируется в терминах свойств того соответствия, к-рое должно иметь место между исходными данными и результатами алгоритма. Важные примеры а. п. : проблема вычисления данной функции (требуется построить алгоритм, вычисляющий эту функцию); проблема разрешения данного множества (требуется построить алгоритм, разрешающий это множество относительно нек-рого другого множества); проблема перечисления данного множества (требуется построить алгоритм, перечисляющий данное множество). Все примеры а. п. из различных областей математики, названные ниже в разделе «Приложения», являются проблемами разрешения. Неразрешимость а. п. означает отсутствие соответствующего алгоритма; теоремы, устанавливающие неразрешимость таких проблем, относятся к числу наиболее важных теорем А. т. Так, для алгоритма с неразрешимой областью применимости неразрешима а. п. разрешения этой области относительно области возможных исходных данных. Посредством сведения к неразрешимости этой проблемы была установлена неразрешимость большинства других проблем разрешения (в частности, всех проблем, указанных ниже в разделе «Приложения»). Вопрос о том, для любой ли неразрешимой проблемы разрешения ее неразрешимость может быть установлена таким способом, составляет так наз. проблему алгоритмической сводимости.

Метрическая теория алгоритмов. А. т. можно разделить на дескриптивную (качественную) и метрическую (количественную). Первая - исследует алгоритмы с точки зрения устанавливаемого ими соответствия между исходными данными и результатами; к ней относятся, в частности, те алгоритмич. проблемы, о к-рых говорилось в предыдущем разделе. Вторая - исследует алгоритмы с точки зрения сложности как самих алгоритмов (см. Алгоритма сложность), так и задаваемых ими «вычислений», то есть процессов последовательного преобразования конструктивных объектов. Важно подчеркнуть, что как сложность алгоритмов, так и сложность вычислений могут определяться различными способами, причем может оказаться, что при одном способе А будет сложнее В, а при другом способе - наоборот. Чтобы говорить о сложности алгоритмов, надо сначала описать к.-л. точный язык для записи алгоритмов и затем под сложностью алгоритма понимать сложность его записи; сложность же записи можно определять различными способами (напр., как число символов данного типа, участвующих в записи, или как набор таких чисел, вычисленных для разных типов символов). Чтобы говорить о сложности вычисления, надо уточнить, как именно вычисление представляется в виде цепочки сменяющих друг друга конструктивных объектов и что считается сложностью такой цепочки (только ли число членов в ней - «число шагов» вычисления, или еще учитывается «размер» этих членов и т. п.); в любом случае сложность вычисления зависит от исходного данного, с к-рого начинается вычисление, поэтому сложность вычисления есть функция, сопоставляющая с каждым объектом из области применимости алгоритма сложность соответствующей цепочки. Разработка методов оценки сложности алгоритмов и вычислений имеет важное теоретич. и практич. значение, однако в отличие от дескриптивной А. т., оформившейся в целостную математич. дисциплину (см. [11], [15], [16]), метрич. А. т. находится в процессе становления (см. [17]-[20]).

Приложения теории алгоритмов имеются во всех областях математики, в к-рых встречаются алгоритмич. проблемы. Такие проблемы возникают в математической логике и моделей теории, для каждой теории формулируется проблема разрешения множества всех истинных или доказуемых предложений этой теории относительно множества всех ее предложений (теории подраз-

деляются на разрешимые и неразрешимые - в зависимости от разрешимости или неразрешимости указанной проблемы); в 1936 А. Чёрч (см. [21], [22]) установил неразрешимость проблемы разрешения для множества всех истинных предложений логики предикатов, дальнейшие важные результаты в этом направлении принадлежат А. Тарскому (A. Tarski), А. И. Мальцеву и др. (см. [23]). Неразрешимые алгоритмич. проблемы встречаются в алгебре (проблема тождества для полугрупп и, в частности, для групп); первые примеры полугрупп с неразрешимой проблемой тождества были найдены в 1947 независимо А. А. Марковым (см. [9]) и Э. Л. Постом (см. [8]), а пример группы с неразрешимой проблемой тождества - в 1952 П. С. Новиковым (см. [24], [25]); в топологии (проблема гомеоморфии, неразрешимость к-рой для важного класса случаев была доказана в 1958 А. А. Марковым, (см. [26]); в теории чисел (проблема разрешимости диофантовых уравнений, неразрешимость к-рой была установлена в 1970 Ю. В. Матиясевичем, (см. [27], [28]) и др. разделах математики.

А. т. тесно связана с математич. логикой, поскольку на понятие алгоритма опирается одно из центральных понятий математич. логики - понятие исчисления, и потому, напр., Гёделя теорема о неполноте формальных систем может быть получена как следствие теорем А. т. (см. [29]). Наконец, А. т. тесно связана с основаниями математики, в к-рых одно из центральных мест занимает проблема соотношения конструктивного и неконструктивного; в частности, А. т. дает аппарат, необходимый для разработки конструктивного направления в математике; в 1965 А. Н. Колмогоров предложил использовать А. т. для обоснования теории информации (см. [30], Алгоритмическая теория информации). А. т. образует теоретич. фундамент для ряда вопросов вычислительной математики и тесно связана с кибернетикой, в которой важное место занимает изучение алгоритмов управления.

Лит. : [1] Вейль Г., О философии математики, пер. с нем., М. - Л., 1934; [2] Church A., «Аmеr. J. Math. », 1936, v. 58, № 2, р. 345-63; [3] Turing A. М., «Рrос. London Math. Soc. », ser. 2, 1936, v. 42, №№ 3-4, p. 230-65; [4] eго же, там же, 1937, v. 43, № 7, p. 544-46; [5] Pоst Е. L., «J. Symbol. Log. », 1936, v. 1, № 3, p. 103-05; [6] eго же, «Аmеr. J. Math. », 1943, v. 65, № 2, p. 197-215; [7] eго же, «Bull. Amer. Math. Soc. », 1944, v. 50, № 5, p. 284-316; [8] его жe, «J. Symbol. Log. », 1947, v. 12, № 1, p. 1-11; [9] Mapков А. А., «Докл. АН СССР», 1947, т. 55, № 7, с. 587-90; [10] его же, «Тр. Матем. ин-та АН СССР», 1951, т. 38, с. 176-89; [11] его же, Теория алгорифмов, М. - Л., 1954; [12] Колмогоров А. Н., «Успехи матем. наук», 1953, т. 8, № 4, с. 175-76; [13] Колмогоров А. Н., Успенский В. А., там же, 1958, т. 13, № 4, с. 3-28; [14] Ершов Ю. Л., Теория нумераций, ч. 1-2, Новосибирск, 1969-73; [15] Мальцев А. И., Алгоритмы и рекурсивные функции, М., 1965; [16] Роджерс X., Теория рекурсивных функций и эффективная вычислимость, пер. с англ., М., 1972; [17] Марков А. А., «Изв. АН СССР. Сер. матем. », 1967, т. 31, № 1, с. 161-208; [18] Трахтенброт Б. А., Сложность алгоритмов и вычислений, Новосибирск, 1967; [19] Проблемы математической логики. Сложность алгоритмов и классы вычислимых функций, сб. переводов, М., 1970; [20] Сложность вычислений и алгоритмов, сб. переводов, М., 1974; [21] Church А., «J. Symbol. Log. », 1936, v. 1, № 1, p. 40-41; [22] его же, там же, № 3, р. 101-02; [23] Ершов Ю. Л., Лавров И. А., Тайманов А. Д., Тайцлин М. А., «Успехи матем. наук», 1965, т. 20, № 4, с. 37-108; [24] Новиков П. С., «Докл. АН СССР», 1952, т. 85, с. 709-12; [25] его же, Об алгоритмической неразрешимости проблемы тождества слов в теории групп, М., 1955; [26] Марков А. А., «Докл. АН СССР», 1958, т. 121, № 2, с. 218-20; [27] Матиясевич Ю. В., там же, 1970, т. 191, № 2, с. 279-82; [28] его же, «Успехи матем. наук», 1972, т. 27, № 5, с. 185-222; [29] Успенский В. А., там же, 1974, т. 29, № 1, с. 3-47; [30] Колмогоров А. Н., «Проблемы передачи информации», 1965, т. 1, № 1, с. 3-11.

В. А. Успенский.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.