
АЛГОРИТМОВ СОЧЕТАНИЯ
Расстановка ударений: АЛГОРИ`ТМОВ СОЧЕТА`НИЯ
АЛГОРИТМОВ СОЧЕТАНИЯ - название, установившееся за рядом конкретных способов конструирования новых алгоритмов из нескольких заданных.
В применении к нормальным алгорифмам наибольшую известность получили следующие А. с: нормальная композиция (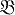 ○
○ 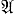 ) двух нормальных алгорифмов
) двух нормальных алгорифмов 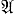 и
и 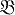 , нормальное объединение (
, нормальное объединение (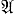 ⌒
⌒ 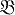 ) двух нормальных алгорифмов
) двух нормальных алгорифмов 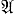 и
и 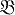 , нормальное разветвление (
, нормальное разветвление (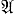 Υ
Υ 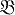 |
|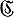 ) двух нормальных алгорифмов
) двух нормальных алгорифмов 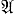 и
и 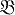 , управляемое нормальным алгорифмом
, управляемое нормальным алгорифмом 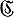 , нормальное повторение (
, нормальное повторение (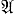

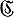 ) нормального алгорифма
) нормального алгорифма 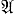 , управляемое нормальным алгорифмом
, управляемое нормальным алгорифмом 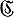 . Если
. Если 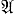 ,
, 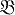 ,
, 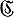 - нормальные алгорифмы в нек-ром алфавите А, то упомянутые их сочетания являются нормальными алгорифмами в нек-ром фиксированном расширении А и удовлетворяют следующим условиям: а) для любого слова Р в А имеет место
- нормальные алгорифмы в нек-ром алфавите А, то упомянутые их сочетания являются нормальными алгорифмами в нек-ром фиксированном расширении А и удовлетворяют следующим условиям: а) для любого слова Р в А имеет место 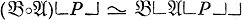 (теорема композиции); б) для любого слова Р в А имеет место
(теорема композиции); б) для любого слова Р в А имеет место 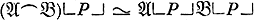 (теорема объединения); в) для любого слова Р в А
(теорема объединения); в) для любого слова Р в А
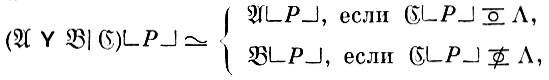
причем если (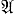 Υ
Υ 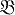 |
|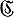 )
) P
P определено, то определено и
определено, то определено и 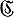
 P
P (теорема разветвления); г) для любых слов Р и Q в А графическое равенство (
(теорема разветвления); г) для любых слов Р и Q в А графическое равенство (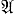

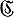 )
) P
P ≖ Q имеет место тогда и только тогда, когда может быть указан ряд слов P0, P1, ..., Pk (k ≥ 1) в алфавите А таких, что
≖ Q имеет место тогда и только тогда, когда может быть указан ряд слов P0, P1, ..., Pk (k ≥ 1) в алфавите А таких, что
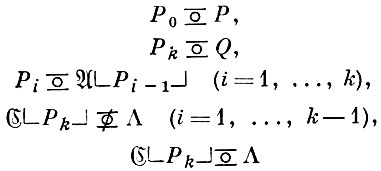
(теорема повторения). Аналогичные теоремы могут быть получены и для Тьюринга машин. В теории рекурсивных функций наибольшее употребление нашли их сочетания, доставляемые оператором подстановки, оператором примитивной рекурсии и μ - оператором.
Теоремы об А. с. вскрывают весьма существенную особенность осуществленных стандартизации общего понятия алгоритма - их «устойчивость» по отношению к естественным способам А. с. Это обстоятельство является одним из наиболее веских доводов в пользу основной гипотезы теории алгоритмов (Чёрча тезиса). Теоремы об А. с. составляют важный раздел общей теории алгоритмов. Будучи доказаны однажды, они позволяют в дальнейшем убеждаться в осуществимости сложных и громоздких алгоритмов без фактического выписывания определяющих их схем.
Значительный интерес для общей теории алгоритмов представляет вопрос о разыскании базиса, позволяющего при фиксированном наборе способов А. с. порождать любой алгоритм к.-л. интересующего нас класса.
Лит. : [1] Марков А. А., Теория алгорифмов, «Тр. Матем. ин-та АН СССР», 1954, т. 42, с. 94-145; [2] Клини С. К., Введение в метаматематику, пер. с англ., М., 1957; [3] Успенский В. А., Лекции о вычислимых функциях, М., 1960; [4] Мальцев А. И., Алгоритмы и рекурсивные функции, М., 1965.
Н. М. Нагорный.
Источники:
- Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'