АЛГОРИТМИЧЕСКАЯ ТЕОРИЯ ИНФОРМАЦИИ

Расстановка ударений: АЛГОРИТМИ`ЧЕСКАЯ ТЕО`РИЯ ИНФОРМА`ЦИИ

АЛГОРИТМИЧЕСКАЯ ТЕОРИЯ ИНФОРМАЦИИ - раздел математич. логики, уточняющий и изучающий на базе понятий алгоритма и вычислимой функции основные понятия теории информации. А. т. и. стремится обосновать эти понятия без помощи обращения к теории вероятностей и так, чтобы понятия энтропии и количества информации были применимы к индивидуальным объектам. Наряду с этим она порождает и свои собственные проблемы, связанные с изучением энтропии конкретных индивидуальных объектов.

Центральным понятием А. т. и. является понятие энтропии индивидуального объекта, называемое сложностью объекта (по Колмогорову). Интуитивно под этим понимается минимальное количество информации, необходимое для восстановления данного объекта. Точное определение понятия сложности индивидуального объекта и на основе этого понятия количества информации в индивидуальном объекте y относительно индивидуального объекта х было дано А. Н. Колмогоровым в 1962-65, что и послужило началом развития А. т. и.

Без существенных ограничений общности можно рассматривать только двоичные слова (что в дальнейшем и будет делаться). Под сложностью слова x понимается длина l(р) самого короткого (двоичного) слова р, содержащего всю информацию, необходимую для восстановления х при помощи к.-л. фиксированного способа декодирования. Точное определение этого понятия следующее.

Пусть F(s) - произвольная словарная частично рекурсивная функция. Тогда под сложностью слова х по F понимается:

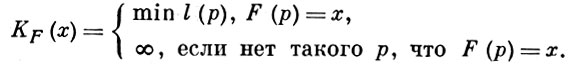
Слово р такое, что F(р) = х, наз. кодом, или программой, по к-рой F восстанавливает слово х. Имеет место теорема: существует частично рекурсивная функция F₀ (называемая оптимальной) такая, что для любой частично рекурсивной функции F выполняется неравенство:

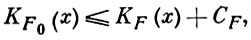
где С_F - константа, не зависящая от х. Эта теорема позволяет дать инвариантное (с точностью до аддитивной константы) определение сложности: сложностью К(х) слова х наз. сложность K_F0 (x) по нек-рой раз и навсегда фиксированной оптимальной частично рекурсивной функции F₀ . Очевидно, К(x) ≤ l{x) + C, где С - константа, не зависящая от х.

Используя K(х), можно определить также сложность К(х, у) пар слов (х, у): для этого пары (х, у) эффективно кодируются в виде одного слова с(х, у), и под сложностью К(х, у) понимается К(с(х, у)).

П. Мартином-Лёфом (P. Martin-Löf) был исследован вопрос о том, как ведет себя сложность начальных кусков бесконечных двоичных последовательностей. Пусть ω_n означает начальный кусок последовательности ω, составленной из первых n знаков. Тогда почти все (относительно меры Лебега) бесконечные двоичные последовательности ω обладают свойствами: а) для бесконечно многих натуральных n справедливо неравенство K(ω_n) ≥ n - с, где с - нек-рая константа; б) для всех натуральных n, больших нек-рого n_ε, K(ω_n) ≥ n - (1 + ε)log₂ n, где ε - произвольное положительное число (теорема Мартина-Лёфа). С другой стороны, для любой последовательности ω существует бесконечно много натуральных n таких, что K(ω_n) ≤ n - log₂ n

Понятие сложности используется также при изучении алгоритмич. проблем. Здесь более естественной является так наз. сложность разрешения слова х. Интуитивно под этим понимается минимальное количество информации, к-рую надо иметь, чтобы по каждому числу i ≤ l(x) найти i-й знак слова х (длину слова х при этом можно и не знать). Точнее, под сложностью разрешения слова х = x₁ x₂ ... x_l(x) по частично рекурсивной функции G(s, t) понимается

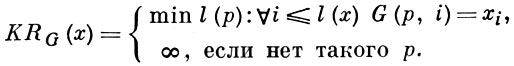
Имеет место теорема: существует частично рекурсивная функция G₀ (называемая оптимальной) такая, что для любой другой частично рекурсивной функции G выполняется неравенство KR_G0 (x) ≤ KR_G (x) + C_G, где C_G - константа, не зависящая от х. Сложностью разрешения KR(x) слова х наз. сложность KR_G0 (x) по нек-рой раз и навсегда фиксированной оптимальной частично рекурсивной функции G₀ . Очевидно, KR(х) ≤ К(х) + С и K(x) ≤ KR(x) + 2l(x) + C. Используя KR(x), можно для любого множества натуральных чисел М определить сложность К(М, n) для n-куска множества М : К(М, n) = KR(ω_n), где ω = x₁ x₂ ... x_i ... - характеристическая последовательность множества М (x_i = 1, если i ∈ M, и x_i = 0, если i ∉ M).

Алгоритмич. проблемы обычно могут быть представлены в виде проблемы вхождения в нек-рое рекурсивно перечислимое множество М. Если мы фиксируем нек-рое n и ограничиваемся рассмотрением проблемы вхождения в М только для первых n натуральных чисел, то мы получаем ограниченную алгоритмическую проблему. Величина К(М, n) интуитивно выражает количество информации, к-рую надо иметь, чтобы можно было решить данную ограниченную проблему. В частности, множество М рекурсивно тогда и только тогда, когда К(М, n) ограничено сверху нек-рой константой.

Из теоремы Мартина-Лёфа следует существование множеств, для к-рых К(М, n)~n. При этом оказывается, что максимально сложные множества уже существуют среди множеств, задаваемых арифметич. предикатами с двумя кванторами. Однако в случае рекурсивно перечислимых множеств имеет место теорема: а) для любого рекурсивно перечислимого множества М и любого n справедливо неравенство К(М, n) ≤ log₂ n + C, где С не зависит от n; б) существует рекурсивно перечислимое множество М такее, что для любого n имеет место неравенство К(М, n) > log₂ n. В то же время существуют такие рекурсивно перечислимые множества М, что при ограничении времени вычислений произвольной общерекурсивной функцией t имеет место оценка К^t (М, n) ≥ n/c_t, где с_t не зависит от n.

В указанных терминах можно дать также характеристику универсальных по нек-рому типу сводимости множеств (см. Универсальное множество): множество М является слабо таблично универсальным тогда и только тогда, когда существует неограниченная общерекурсивная функция f(n) такая, что для любого n имеет место неравенство К(М, n) ≥ f(n).

При изучении сложности ограниченных алгоритмич. проблем иногда используются и другие меры сложности, как, напр., минимальная длина изображения нормального алгорифма, решающего данную ограниченную проблему. Но оказывается, что между введенными выше сложностями и аналогами этих сложностей, выраженными через минимальную длину изображения нормального алгорифма (или через минимальное число внутренних состояний машины Тьюринга), существуют асимптотически точные соотношения (см. Алгоритма сложность).

При построении А. т. и. вводится еще понятие условной сложности слова x при известном y по частично рекурсивной функции G(s, t):

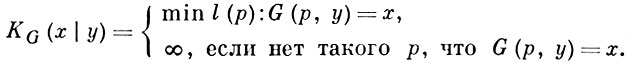
Для этого понятия также имеет место теорема о существовании оптимальной функции G₀, и условная сложность K(х|у) слова x при известном y определяется как сложность K_G0 (x|y) по нек-рой раз и навсегда фиксированной оптимальной функции G₀ ; К(х|у) интуитивно обозначает минимальное количество информации, к-рое необходимо добавить к информации, содержащейся в слове у, чтобы можно было восстановить слово х. Очевидно, К(х|у) ≤ К(х) + С.

Следующим центральным понятием А. т. и. является понятие количества информации в индивидуальном объекте у относительно индивидуального объекта х:

I(у : х) = К(х) - К(х|у).

Величину I (у : х) наз. алгоритмическим количеством информации в у об х. Соответственно величины K(х) и К(х|у) наз. иногда алгоритмической энтропией х и алгоритмической условной энтропией х при заданном у. Формулы разложения энтропии H(X, Y) = H(Х) + Н(Y|X) и коммутативности информации I(X : Y) = I(Y : X) верны в алгоритмич. концепции лишь с точностью до членов порядка O(logH(X, Y)):

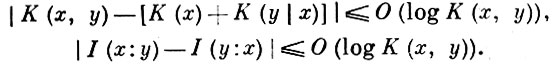
Между алгоритмич. и классич. определениями количества информации (точнее, между сложностью слова по Колмогорову и энтропией распределения частот по Шеннону) существует определенная связь (А. Н. Колмогоров): пусть задано число r и пусть слово х длины i ⋅ r состоит из i слов длины r, причем k-е слово длины r входит в x с частотой q_k (k = 1, 2, ..., 2^r), тогда

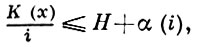
где

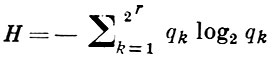
и α (i) → 0 при i → ∞. В общем случае более тесную связь между энтропией и сложностью установить нельзя. Это объясняется тем, что энтропия приспособлена для изучения текстов, не имеющих других закономерностей, кроме частотных. Следовательно, для случайных последовательностей ω по мере, соответствующей независимым испытаниям, между рассматриваемыми величинами можно установить полную связь;

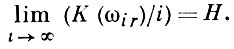
Аналогичный факт имеет место и для произвольного эргодического стационарного случайного процесса.

Лит. : [1] Колмогоров А. Н., «Проблемы передачи информации», 1965, т. 1, вып. 1, с. 3-11; [2] его же, «Проблемы передачи информации», 1969, т. 5, вып. 3, с. 3-7; [3] Звонкин А. К., Левин Л. А., «Успехи матем. наук», 1970, т. 25, вып. 6, с. 85-127; [4] Барздинь Я. М., «Докл. АН СССР», 1968, т. 182, № 6, с. 1249-1252; [5] Канович М. И., «Докл. АН СССР», 1970, т. 194, № 3, с. 500-503.

Я. М. Барздинь.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.