АЛГОРИТМИЧЕСКАЯ СВОДИМОСТЬ

Расстановка ударений: АЛГОРИТМИ`ЧЕСКАЯ СВОДИ`МОСТЬ

АЛГОРИТМИЧЕСКАЯ СВОДИМОСТЬ - одно из основных понятий алгоритмов теории и ее приложений, Возникло в связи с тем, что неразрешимость (и разрешимость) многих алгоритмических проблем устанавливается большей частью не непосредственно, а путем сведения к исследуемой проблеме такой алгоритмич. проблемы, неразрешимость к-рой уже доказана (или исследуемой проблемы к нек-рой уже решенной проблеме). Так, неразрешимость проблемы гомотопии путей в полиэдре доказывается путем сведения к ней проблемы равенства слов в соответствующей фундаментальной группе.

Ниже приведены простейшие примеры А. с. теоретико-числовых (т. е. определенных на натуральных числах) предикатов и функций:

P(x) ≡ Q(2x + 1),

где Р и Q - предикаты. Проблема разрешения предиката Р, т. е. установления истинности и ложности Р для разных х, сводится к проблеме разрешения Q, или, короче, Р сводится к Q. Говорят также, что множество истинности Р, т. е. {х|Р (х)} = M_P, сводится к M_Q = {х|Q(х)}.

Пусть

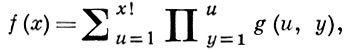
где f(x) и g(u, y) - теоретико-числовые функции. Проблема вычисления функции f сводится к проблеме вычисления g, или, короче, f сводится к g.

Понятие А. с. было уточнено А. М. Тьюрингом (А. М. Turing): если, грубо говоря, нек-рая Тьюринга машина перерабатывает последовательность закодированных значений функции g в последовательность закодированных значений функции f, то функция f сводится к функции g. Близкое понятие относительной вычислимости С. К. Клини (S. С. Kleene) уточнил с помощью рекурсивных схем равенств (см. [1]). После арифметизации каждая алгоритмич. проблема сводится к проблеме вычисления нек-рой теоретико-числовой функции f. Если f сводится к g по Тьюрингу, f ≤_T g, a g сводится к f, g ≤_T f то говорят, что f и g имеют одну и ту же степень неразрешимости, или f ≡_T g. Отношение ≤_T рефлексивно и транзитивно. Таким образом, все функции (и множества натуральных чисел или их характеристич. предикаты) разбиваются на классы эквивалентности, наз. тьюринговыми степенями или Т-степенями (см. [3]). Большинство алгоритмич. проблем, рассматриваемых в логике и математике, являются проблемами разрешения (рекурсивно) перечислимых множеств конструктивных объектов. В связи с этим Э. Л. Пост [2] в 40-х гг. 20 в. предпринял исследование перечислимых множеств и ввел наряду с тьюринговой нек-рые специальные виды А. с., сформулировав проблему (сводимости): сводятся ли (по Тьюрингу) друг к другу различные перечислимые неразрешимые множества? Позже было установлено, что перечислимые множества образуют бесконечную весьма богатую систему T-степеней. При этом был найден так наз. метод приоритета, широко используемый в теории алгоритмов.

В дальнейшем степени неразрешимости нашли применение в других областях математики. Так, напр., для всяких T-степеней а и b перечислимых множеств при а ≤_T b существует конечно определенная группа, в к-рой проблема равенства слов имеет степень a, а проблема сопряженности - степень b. Имеется тесная связь между степенями (относительно различных видов А. с.) перечислимых множеств и скоростью роста сложности начальных фрагментов перечислимых множеств. Специальный вид сводимости - полиномиальная сводимость, или р-сводимость (сводимость с нек-рым ограничением на время), - используется при доказательстве универсальности алгоритмич. проблем «переборного типа», т. е. проблем комбинаторного характера из разных областей математики (см. [5]; более подробную лит. см. в [1]). В свою очередь, при исследовании степеней стали применять методы теории меры (см. [1], гл. 16) и вынуждения метод (см. [4]).

Лит. : [1] Роджерс X., Теория рекурсивных функций и эффективная вычислимость, пер. с англ., М., 1972, гл. 9, 10, 13, 16; [2] Post Е. L., «Bull. Amer. Math. Soc. », 1944, v. 50, № 5, p. 284-316; [3] Кleene S. C., Post E. L., «Ann. Math. », ser. 2, 1954, v. 59, № 3, p. 379-407; [4] Selman A. L., «Рrос. Lond. Math. Soc. », ser. 3, 1972, v. 25, № 4, p. 586-602; [5] Карп P., в кн. : Кибернетический сборник, в. 12, М., 1975.

А. А. Мучник.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.