АЛГОРИТМА СЛОЖНОСТЬ

Расстановка ударений: АЛГОРИ`ТМА СЛО`ЖНОСТЬ

АЛГОРИТМА СЛОЖНОСТЬ описания - величина, характеризующая длину описания алгоритма. В зависимости от точной концепции алгоритма А. с. описания уточняется по-разному. Единого достаточно устоявшегося уточнения к настоящему моменту (1977) не существует. Ниже рассмотрены наиболее часто встречающиеся случаи.

Под сложностью описания нормального алгорифма обычно понимают длину его изображения, т. е. длину записи всех его формул подстановок в одну строку (между формулами проставляется специальная разделительная буква). Под сложностью описания Тьюринга машины обычно понимают число ее внутренних состояний и внешних символов. Иногда для характеристики сложности машины Тьюринга используют число команд данной машины. Для рекурсивных функций, задаваемых схемами рекурсий, в качестве меры сложности обычно используют число букв в этих схемах.

Предложено также и аксиоматическое определение А. с. описания (см. [2]). Рассмотрим это определение применительно к машинам Тьюринга. Пусть (М_i), i = 0, 1, 2, ..., - естественная нумерация машин Тьюринга, характеризующаяся тем, что по номеру машины можно эффективно восстановить саму машину (т. е. ее программу), а по машине (т. е. программе) - ее номер. Общерекурсивная функция s наз. мерой сложности машин (при этом s(i) наз. сложностью машины М_i) тогда и только тогда, когда: а) для любого y существует не более чем конечное число машин, имеющих сложность y; б) существует эффективная процедура, позволяющая определить для любого y все те машины, к-рые имеют сложность y.

Пусть s - произвольная мера сложности машин Тьюринга. Если U - произвольный эффективно (т. е. алгоритмически) перечислимый бесконечный подкласс машин Тьюринга, то существует машина Т, принадлежащая U, и существует машина Т' (не обязательно из U) такая, что Т' и Т вычисляют одну и ту же функцию, и сложность Т' значительно меньше, чем сложность Т. Отсюда, в частности, вытекает существование примитивно рекурсивных функций, наименьшая сложность к-рых в примитивно рекурсивной форме (т. е. через схемы примитивной рекурсии) значительно больше, чем их наименьшая сложность в общерекурсивной форме (т. е. через схемы общей рекурсии). Пусть под сложностью нормальных алгорифмов и машин Тьюринга понимаются, соответственно, длина изображения и число внутренних состояний. Тогда любую функцию алгебры логики от N переменных (см. Булева функция) можно реализовать (см. [3]): а) нормальным алгорифмом в m-буквенном алфавите со сложностью ~2^N /log₂ m; б) машиной Тьюринга с m-буквенным внешним алфавитом со сложностью ~2^N /N(m - 1).

С 60-х гг. 20 в. начато изучение сложности алгоритмов, решающих конечные куски алгоритмически неразрешимых массовых проблем (так наз. ограниченные алгоритмич. проблемы). А. А. Марков рассмотрел следующую задачу: для любой функции алгебры логики от N переменных построить изображение нормального алгорифма в алфавите Ф = {0, 1, а, b, с), реализующего данную функцию и имеющего минимальную сложность среди всех таких алгорифмов. Показано (см. [1], [4]), что сложность нормального алгорифма, решающего эту задачу, имеет порядок 2^N . Изучен также вопрос о сложности алгоритмов, решающих для первых n натуральных чисел проблему вхождения в рекурсивно перечислимое множество (сложность n-кусков рекурсивно перечислимых множеств). Показано, что в случае нормальных алгорифмов эта сложность по порядку не превосходит log₂ n и что в общем случае эта оценка не может быть понижена. В то же время существуют множества, задаваемые с помощью достаточно простых логич. средств, к-рые имеют сложность n-кусков порядка n. Показано также, что при общерекурсивном ограничении времени работы алгорифмов сложность n-кусков рекурсивно перечислимых множеств может возрастать экспоненциально и по порядку достичь величины n.

Понятие А. с. описания используется в основном при уточнении вопроса о том, какова минимальная сложность алгоритма, строящего тот или иной конечный объект. Эту минимальную сложность часто наз. просто сложностью конечного объекта (при данном уточнении понятия А. с. описания).

Определение сложности конечных объектов впервые было предложено А. Н. Колмогоровым (см. Алгоритмическая теория информации). Оказывается, что между сложностью K(х) по Колмогорову, сложностью М_m (х) этих же объектов, выражаемой через длину изображения нормального алгорифма в m-буквенном алфавите, и сложностью Т_m (х), выражаемой числом внутренних состояний машины Тьюринга с m-буквенным внешним алфавитом, существуют асимптотически точные соотношения:

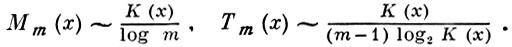
Лит. : [1] Mapков А. А., «Изв. АН СССР. Сер. матем. », 1967, т. 31, № 1, с. 168-208; [2] Блюм М., сб. «Проблемы математической логики», М., 1970, с. 423-31; [3] Кузьмин В. А., сб. «Проблемы кибернетики», 1965, вып. 13, с. 75-96; [4] Петри Н. В., «Докл. АН СССР», 1969, т. 185, № 1, с. 37-39; [5] Звонкин А. К., Левин Л. А., «Успехи матем. наук», 1970, т. 25, вып. 6, с. 85-127.

Я. М. Барздинь.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.