АЛГЕБРАИЧЕСКОЙ СИСТЕМЫ АВТОМОРФИЗМ

Расстановка ударений: АЛГЕБРАИ`ЧЕСКОЙ СИСТЕ`МЫ АВТОМОРФИ`ЗМ

АЛГЕБРАИЧЕСКОЙ СИСТЕМЫ АВТОМОРФИЗМ - изоморфное отображение алгебраической системы на себя. Автоморфизмом (А.) Ω-системы А = 〈 A, Ω 〉 наз. всякое взаимно однозначное отображение φ множества А на себя, обладающее свойствами:

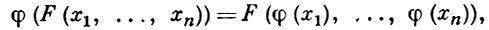
(1)

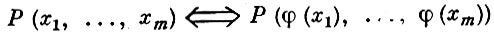
(2)

для всех х₁, х₂,... из А и для всех F, Р из Ω. Другими словами, А. Ω-системы А есть изоморфное отображение системы А на себя. Пусть G - множество всех А. системы А . Если φ ∈ G, то обратное отображение φ^{- 1} также обладает свойствами (1), (2) и поэтому φ^{- 1} ∈ G. Произведение α = φ ψ А. φ, ψ системы А, определяемое формулой α (x) = ψ (φ (х)), х ∈ А, снова является А. системы А . Поскольку умножение отображений ассоциативно, то 〈 G, ⋅, ^{- 1} 〉 есть группа, наз. группой всех А. системы А и обозначаемая через Aut (А ). Подгруппы группы Aut (А ) наз. просто группами А. системы А .

Пусть φ - А. системы А и θ - конгруэнция этой системы. Полагая

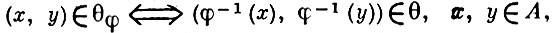
получим снова конгруэнцию θ_φ системы А . А. φ наз. IC-автоморфизмом, если θ_φ = θ для любой конгруэнции θ системы А . Множество IС(А ) всех IС-автоморфизмов системы А является нормальным делителем группы Aut(А ), и факторгруппа Aut(А )/IC(А ) изоморфна нек-рой группе А. решетки всех конгруэнции системы А [1]. В частности, всякий внутренний А. х → а^{- 1} ха группы, определяемый к.-л. фиксированным элементом а этой группы, является IC-автоморфизмом. Однако пример циклич. группы простого порядка показывает, что не всякий IС-автоморфизм группы - внутренний.

Пусть - нетривиальное многообразие Ω-систем или к.-л. другой класс Ω-систем, обладающий свободными системами любого (ненулевого) ранга. А. φ системы А из класса наз. I-автоморфизмом, если существует терм f_φ (x₁, ..., x_n) сигнатуры Ω от неизвестных x₁, ..., x_n, для к-рого: 1) в системе А существуют такие элементы a₁, ..., a_n, что для каждого; элемента х ∈ А имеет место равенство

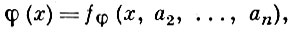
2) для любой системы B из класса отображение

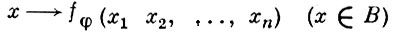
является А. этой системы при любом выборе элементов x₂, ..., x_n в системе B . Множество I(А ) всех I-автоморфизмов каждой системы А из класса является нормальным делителем группы Aut (А ). В классе. всех групп понятие I-автоморфизма совпадает с понятием внутреннего А. группы [2]. Более общее понятие формульного А. Ω-системы см. в [3].

Пусть А - алгебраич. система. Заменяя каждую основную операцию F в А предикатом

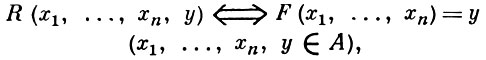
получим так наз. модель А *, представляющую систему А . Справедливо равенство Aut (А *) = Aut (А ). Если системы А = 〈 А, Ω 〉, А ' = 〈 A, Ω ' 〉 имеют общий носитель А и Ω ⊂ Ω ', то Aut (А ) ⊇ Aut (А '). Если Ω-система А с конечным числом порождающих финитно аппроксимируема, то группа Aut (А ) также финитно аппроксимируема (см. [1], с. 432). Пусть - класс Ω-систем и пусть Aut () - класс всех изоморфных копий групп Aut (А ), А ∈ , a SAut () - класс подгрупп групп из класса Aut(). Класс SAut () состоит из групп, изоморфно вложимых в группы Aut (А ), А ∈ .

В исследовании групп А. алгебраич. систем выделились следующие две проблемы.

1) Пусть дан класс Ω-систем. Что можно сказать о классах Aut () и SAut ()?

2) Пусть дан (абстрактный) класс К групп. Существует ли класс Ω-систем данной сигнатуры Ω такой, что K = Aut () или хотя бы K = SAut ()? Доказано, что для любого аксиоматизируемого класса моделей класс групп SAut () универсально аксиоматизируем [1]. Доказано также [1], [4], что если - аксиоматизируемый класс моделей, имеющий бесконечные модели, 〈 B, ≤ 〉 - линейно упорядоченное множество и G - группа А. модели 〈 B, ≤ 〉, то существует модель А ∈ такая, что A ⊇ В и для каждого элемента g ∈ G существует А. φ системы А такой, что g(х) = φ (х) для всех х ∈ B. Группа G наз. : 1) универсальной, если G ∈ Aut () для любого аксиоматизируемого класса моделей, обладающего бесконечными моделями; 2) группой порядковых А. упорядочиваемой группы H (см. Линейно упорядоченная группа), если G изоморфна нек-рой группе А. группы H, сохраняющих фиксированный линейный порядок ≤ этой группы (т. е. а ≤ b ⇒ φ (а) ≤ φ (b) для всех а, b ∈ Н, φ ∈ G).

Пусть l - класс линейно упорядояенных множеств 〈 M, ≤ 〉, U - класс универсальных групп, RO - класс правоупорядочиваемых групп, OA - класс групп порядковых А. свободных абелевых групп. Тогда (см. [4]-[6]):

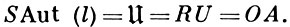
Каждая группа изоморфна группе всех А. нек-рой Ω-алгебры. Если - класс всех колец, то Aut () - класс всех групп (см. [1], с. 117, 118). Но если - класс всех групп, то Aut() ≠ ; напр., циклич. группы C₃, C₅, C₇ порядков 3, 5, 7, соответственно, не принадлежат классу Aut (). Не существует также топологич. группы, для к-рой группа всех топологич. А. была бы изоморфна группе C₅ (см. [7]).

Лит. : [1] Плоткин Б. И., Группы автоморфизмов алгебраических систем, М., 1966; [2] Csákány В., «Рubl. Math. Debrecen», 1965, v. 12, p. 331-33; [3] Grant I., «Pacif. J. Math. », 1973, v. 44, № 1, p. 107-15; [4] Rabin M. O., в кн. : The theory of models, Amst., 1965, p. 274-84; [5] Соhn Р. M., «Mathematika», 1957, v. 4, № 7, p. 41-50; [6] Смирнов Д. M., «Алгебра и логика», 1966, т. 5, № 6, с. 41-59; [7] Willе R. J., «Quart. J. Math. Oxford», ser. 2, 1967, v. 18, № 69, p. 53-57.

Д. M. Смирнов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.