НОВОСТИ БИБЛИОТЕКА ЭНЦИКЛОПЕДИЯ БИОГРАФИИ КАРТА САЙТА ССЫЛКИ О ПРОЕКТЕ

АЛГЕБРАИЧЕСКОЕ СРАВНЕНИЕ

Расстановка ударений: АЛГЕБРАИ`ЧЕСКОЕ СРАВНЕ`НИЕ

АЛГЕБРАИЧЕСКОЕ СРАВНЕНИЕ - сравнение вида:

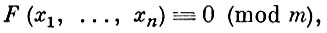
(1)

где

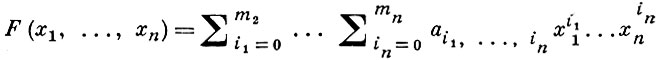
- многочлен от переменных x₁, ..., x_n с целыми рациональными коэффициентами a_i₁, ..., a_{i_n} . Максимальное значение величины

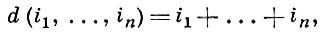
где максимум берется по всевозможным наборам i₁, ..., i_n, для к-рых a_i₁, ..., a_{i_n} ≢ 0 (mod m), наз. степенью по совокупности переменных x₁, ..., x_n, или степенью алгебраического сравнения (1). Максимальное значение величины i_s, 1 ≤ s ≤ n, где максимум берется по тем же наборам i₁, ..., i_n, наз. степенью алгебраического сравнения (1) по переменной x_s .

Основным вопросом в теории А. с. является вопрос о числе решений того или иного сравнения. При этом можно ограничиться лишь случаем простого модуля, поскольку вопрос о числе решений А. с. (1) по составному модулю m, за исключением нек-рых вырожденных случаев, сводится к вопросу о числе решений сравнений F(x₁, ..., x_n) ≡ 0 (mod р) по простым модулям р, делящим m.

Среди А. с. F(x) ≡ 0 (mod р) от одной переменной наиболее изучены двучленные сравнения

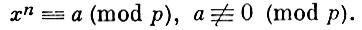
Исследование вопроса о числе решений сравнения в случае многочлена F(х) общего вида встречает значительные трудности и при его решении получены лишь отдельные частные результаты.

Систему сравнений

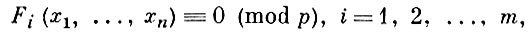
(2)

можно трактовать как систему алгебраич. уравнений:

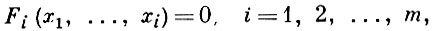
над простым конечным полем ℤ /(р), состоящим из р элементов; число решений этой системы сравнений будет числом ℤ /(р) - рациональных точек алгебраического многообразия, определяемого системой уравнений (2). Поэтому, наряду с теоретико-числовыми методами, к изучению А. с. или систем А. с. применяются методы алгебраич. геометрии.

Среди А. с. от нескольких переменных более полно исследованы сравнения вида

F (х, у) ≡ 0 (mod р).

Именно, для числа решений N_p А. с. этого вида, где F(x, у) - абсолютно неприводимый многочлен, получена оценка

Здесь константа g зависит лишь от многочлена и равна роду кривой F(x, у) = 0. В первом нетривиальном случае - для эллиптич. сравнения

у² ≡ х³ + ах + b (mod p).

такую оценку получил X. Хассе (Н. Hasse) в 1934, основываясь на формуле сложения точек Якоби многообразия кривой у² = х³ + ах + b. Позже метод Хассе был распространен А. Вейлем [4] на случай абсолютно неприводимых многочленов F. В [3] указанная оценка была получена с помощью элементарных методов.

А. с. с числом переменных n ≥ 3 изучены значительно слабее. В качестве общего результата можно отметить теорему Шевалле, утверждающую, что если F(x₁, ..., x_n) - форма, степень к-рой строго меньше числа переменных, то число решений сравнения

F (x₁, ..., x_n) = 0 (mod p)

положительно и делится на р; для однородных многочленов существование решения не гарантируется; но делимость на р остается в силе (теорема Варнинга). Существуют обобщения последней теоремы на случай систем сравнений. Теория А. с. имеет многочисленные применения в других разделах теории чисел - в теории диофантовых уравнений, задачах аддитивной теории чисел, теории алгебраич. чисел и т. д.

Лит. : [1] Боревич 3. И., Шафаревич И. Р., Теория чисел, 2 изд., М., 1972; [2] Виноградов И. М., Основы теории чисел, 8 изд., М., 1972; [3] Степанов С. А., «Труды Матем. ин-та АН СССР», 1973, т. 132, с. 237-46; [4] Weil A., Sur les courbes algébriques et les variétés qui s'en déduisent, P., 1948.

С. А. Степанов.

Источники:

Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.

ПОИСК:

© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'