АЛГЕБРАИЧЕСКОГО МНОГООБРАЗИЯ АВТОМОРФИЗМ

Расстановка ударений: АЛГЕБРАИ`ЧЕСКОГО МНОГООБРА`ЗИЯ АВТОМОРФИ`ЗМ

АЛГЕБРАИЧЕСКОГО МНОГООБРАЗИЯ АВТОМОРФИЗМ - обратимый морфизм алгебраич. многообразия (или схемы) в себя. Группа всех А. м. а., обозначаемая обычно Aut X, - важный инвариант многообразия X. Изучение действий группы А. м. а. на объектах, функториально связанных с X, таких, как Пикара группа, Чжоу кольцо, К-функтор, группа когомологий, является средством изучения самих многообразий. Группа А. м. а. участвует при образовании форм алгебраич. многообразия. Для полных алгебраич. многообразий над полем комплексных чисел группа А. м. а. совпадает с группой биголоморфных автоморфизмов.

Для ряда простых алгебраич. многообразий строение группы Aut X известно. Напр., если X проективное n-мерное пространство Рⁿ над полем k, то любой его автоморфизм является линейным проективным преобразованием и Aut Рⁿ совпадает с проективной линейной группой PGL(n + 1, k). Группа автоморфизмов эллиптич. кривой и, вообще, любого абелева многообразия А является расширением группы G автоморфизмов, сохраняющих структуру абелева многообразия, при помощи группы А(k) сдвигов на точки многообразия А, т. е. последовательность групп

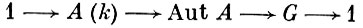
точна. Если X - гладкая полная алгебраич. кривая рода g > 1, то группа Aut X конечна; известна оценка ее порядка в зависимости от g (см. Алгебраическая кривая). Об автоморфизмах поверхностей см. Алгебраическая поверхность.

Для алгебраич. многообразий с обильным канонич. или антиканонич. обратимым пучком группа автоморфизмов является алгебраич. подгруппой группы PGL (N, k) для нек-рого N. Группа автоморфизмов гладкой поверхности размерности n ≥ 2 и степени конечна [1].

Во всех приведенных выше примерах Aut X обладает естественной структурой алгебраич. группы, быть может, с бесконечным числом связных компонент; это верно и в общем случае [2].

Современный подход к изучению группы А. м. а. состоит в рассмотрении семейств автоморфизмов. Семейством автоморфизмов многообразия X со схемой параметров Т наз. автоморфизм произведения X × T, перестановочный с проекцией на второй множитель; множество семейств автоморфизмов со схемой параметров Т обозначается Aut_T (X × T). Сопоставление T| → Aut_T (X × T) является контравариантным функтором от Т. Если многообразие X полное, то этот функтор представим (см. Представимый функтор) локально алгебраич. схемой групп с не более чем счетным числом связных компонент [3]. Для проективных многообразий этот факт был доказан А. Гротендпком (A. Grothendieck); существует обобщение этой теоремы на случай собственных плоских морфизмов схем. Представляющая схема не обязательно является приведенной, даже в случае, когда X - гладкая проективная поверхность; однако, если характеристика основного поля равна 0, либо если X - гладкая кривая или гладкая гиперповерхность, то связная компонента единицы этой схемы является многообразием.

Для неполных многообразий функтор автоморфизмов не всегда представим в категории схем. Для аффинного многообразия функтор автоморфизмов представим в категории индуктивных пределов схем.

Для аффинных пространств, кроме простого случая аффинной прямой, известна только группа автоморфизмов аффинной плоскости. Она является свободным произведением с объединенным пересечением двух своих подгрупп - подгруппы линейных аффинных преобразований и подгруппы треугольных автоморфизмов, т. е. преобразований вида

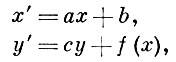
где a, b, с ∈ k, а ≠ 0, с ≠ 0, a f(x) - произвольный многочлен от х (см. [4], [5]). Об аффинных алгебраич. поверхностях, на к-рых группа автоморфизмов действует транзитивно, см. [6].

Лит. : [1] Matsumura Н., Моnsку P., «J. Math. Kyoto Univ. », 1964, v. 3, p. 347-61; [2] Matsusака Т., «Аmеr. J. Math. », 1958, v. 80, № 1, p. 45-82; [3] Matsumura H., Ооrt F., «Invent Math. », 1967, v. 4, № 1, p. 1-25; [4] Engel W., «Math. Ann. », 1958, v. 136, p. 319-25; [5] Shafarevich I. R., «Rend. Math. », 1966, v. 25, p. 208-12; [6] Гизатуллин М. X., «Изв. АН СССР. Сер. матем. », 1971, т. 35, № 5, с. 1047-71; [7] Roth L., Algebraic threefolds, В. - [u. a.], 1955.

В. И. Данилов, В. А. Исковских.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.