
АЛГЕБРАИЧЕСКИХ СИСТЕМ МНОГООБРАЗИЕ
Расстановка ударений: АЛГЕБРАИ`ЧЕСКИХ СИСТЕ`М МНОГООБРА`ЗИЕ
АЛГЕБРАИЧЕСКИХ СИСТЕМ МНОГООБРАЗИЕ - алгебраических систем класс фиксированной сигнатуры Ω, аксиоматизируемый при помощи тождеств, т. е. формул вида
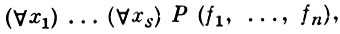
где Р - к.-л. предикатный символ из Ω или знак равенства, f1, ..., fn - термы сигнатуры Ω от предметных переменных x1, ..., xs . А. с. м. наз. иначе эквациональными классами, иногда примитивными классами. Многообразие сигнатуры Ω может быть определено также (теорема Биркгофа) как непустой класс Ω-систем, замкнутый относительно подсистем, гомоморфных образов и декартовых произведений.
Пересечение всех многообразий сигнатуры Ω, содержащих данный (не обязательно абстрактный) класс 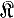 Ω-систем, наз. эквациональным замыканием класса
Ω-систем, наз. эквациональным замыканием класса 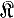 (или многообразием, порожденным классом
(или многообразием, порожденным классом 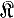 ) и обозначается var
) и обозначается var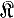 . В частности, если класс
. В частности, если класс 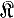 состоит из одной Ω-системы А, то его эквациональное замыкание обозначают varА . Если система А конечна, то все конечно порожденные системы в многообразии varА также конечны [1], [2].
состоит из одной Ω-системы А, то его эквациональное замыкание обозначают varА . Если система А конечна, то все конечно порожденные системы в многообразии varА также конечны [1], [2].
Пусть ℒ - нек-рый класс Ω-систем, Sℒ - класс подсистем систем из ℒ, Нℒ - класс гомоморфных образов систем из ℒ, Пℒ - класс изоморфных копий декартовых произведений систем из ℒ. Для произвольного непустого класса 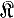 Ω-систем имеет место соотношение (см. [1], [2]):
Ω-систем имеет место соотношение (см. [1], [2]):
var 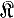 = HSПℒ.
= HSПℒ.
Многообразие наз. тривиальным, если в каждой его системе истинно тождество х = у. Всякое нетривиальное многообразие  обладает свободными системами Fm
обладает свободными системами Fm ) любого ранга m и
) любого ранга m и  = var F
= var F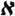 0 (
0 ( ) (см. [1], [2]).
) (см. [1], [2]).
Пусть S - множество тождеств сигнатуры Ω и KS - класс всех Ω-систем, в к-рых истинны все тождества из S. Если для многообразия  сигнатуры Ω выполняется равенство
сигнатуры Ω выполняется равенство  = KS, то S наз. базисом для
= KS, то S наз. базисом для  . Многообразие
. Многообразие  наз. конечно базируемым, если оно имеет конечный базис S. Для любой системы А базис многообразия varА наз. также базисом тождеств системы А . Если
наз. конечно базируемым, если оно имеет конечный базис S. Для любой системы А базис многообразия varА наз. также базисом тождеств системы А . Если  - конечно базируемое многообразие алгебр конечной сигнатуры и все алгебры из
- конечно базируемое многообразие алгебр конечной сигнатуры и все алгебры из  имеют дистрибутивные решетки конгруэнции, то каждая конечная алгебра А из
имеют дистрибутивные решетки конгруэнции, то каждая конечная алгебра А из  имеет конечный базис тождеств (см. [10]). В частности, любая конечная решетка 〈 А, ∨, ∧ 〉 обладает конечным базисом тождеств. Конечный базис тождеств имеет любая конечная группа [3]. Напротив, существует 6-элементная полугруппа [5] и 3-элементный группоид [6], у к-рых нет конечного базиса тождеств.
имеет конечный базис тождеств (см. [10]). В частности, любая конечная решетка 〈 А, ∨, ∧ 〉 обладает конечным базисом тождеств. Конечный базис тождеств имеет любая конечная группа [3]. Напротив, существует 6-элементная полугруппа [5] и 3-элементный группоид [6], у к-рых нет конечного базиса тождеств.
Многообразия Ω-систем, содержащиеся в к.-л. фиксированном многообразии  сигнатуры Ω, составляют по включению полную решетку L(
сигнатуры Ω, составляют по включению полную решетку L( ) с нулем и единицей, к-рая наз. решеткой подмногообразий многообразия
) с нулем и единицей, к-рая наз. решеткой подмногообразий многообразия  . Нулем этой решетки служит многообразие с базисом х = у, Р(x1, ..., x) (P ∈ Ω), а единицей - многообразие
. Нулем этой решетки служит многообразие с базисом х = у, Р(x1, ..., x) (P ∈ Ω), а единицей - многообразие  . Если многообразие
. Если многообразие  нетривиально, то решетка L(
нетривиально, то решетка L( ) антиизоморфна решетке всех вполне характеристических конгруэнции свободной в
) антиизоморфна решетке всех вполне характеристических конгруэнции свободной в  системы F
системы F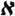 0 (
0 ( ) счетного ранга [1]. Решетка LΩ всех многообразий сигнатуры Ω бесконечна, кроме случая, когда множество Ω конечно и состоит лишь из предикатных символов. Известно точное значение мощности бесконечной решетки LΩ (см. [1]). Решетка всех многообразий решеток 〈 L, ∧, ∨ 〉 дистрибутивна и имеет мощность континуума [7], [8]. Решетка всех многообразий групп 〈 G, ⋅, - 1 〉 модулярна, но не дистрибутивна [3], [4]. Решетка многообразий коммутативных полугрупп не модулярна [9].
) счетного ранга [1]. Решетка LΩ всех многообразий сигнатуры Ω бесконечна, кроме случая, когда множество Ω конечно и состоит лишь из предикатных символов. Известно точное значение мощности бесконечной решетки LΩ (см. [1]). Решетка всех многообразий решеток 〈 L, ∧, ∨ 〉 дистрибутивна и имеет мощность континуума [7], [8]. Решетка всех многообразий групп 〈 G, ⋅, - 1 〉 модулярна, но не дистрибутивна [3], [4]. Решетка многообразий коммутативных полугрупп не модулярна [9].
Атомы решетки LΩ всех многообразий сигнатуры Ω наз. минимальными многообразиями сигнатуры Ω. Каждое многообразие, обладающее неединичной системой, содержит хотя бы одно минимальное многообразие. Если Ω-система А конечна и конечного типа, то многообразие varА содержит лишь конечное число минимальных подмногообразий [1].
Пусть 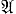 ,
, 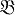 - подмногообразия фиксированного многообразия
- подмногообразия фиксированного многообразия  Ω-систем. Мальцевским произведением
Ω-систем. Мальцевским произведением 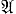
 ○
○ 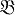 наз. класс тех систем А из
наз. класс тех систем А из  , к-рые обладают такой конгруэнцией θ, что (A /θ) ∈
, к-рые обладают такой конгруэнцией θ, что (A /θ) ∈ 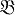 , а все смежные классы а/θ (а ∈ А ), являющиеся системами из
, а все смежные классы а/θ (а ∈ А ), являющиеся системами из  , принадлежат
, принадлежат 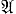 . Если
. Если  - многообразие всех групп, а
- многообразие всех групп, а 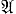 ,
, 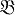 - его подмногообразия, то произведение
- его подмногообразия, то произведение 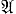
 ○
○ 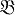 совпадает с произведением в смысле X. Нейман [3]. Произведение многообразий полугрупп может не быть многообразием. Многообразие
совпадает с произведением в смысле X. Нейман [3]. Произведение многообразий полугрупп может не быть многообразием. Многообразие  Ω-систем наз. поляризованным, если существует такой терм е(х) сигнатуры Ω, что в каждой системе из
Ω-систем наз. поляризованным, если существует такой терм е(х) сигнатуры Ω, что в каждой системе из  истинны тождества е(х) = е(у), F(e(x), ..., е(х)) = е(х) (F ∈ Ω). Если
истинны тождества е(х) = е(у), F(e(x), ..., е(х)) = е(х) (F ∈ Ω). Если  - поляризованное многообразие алгебр и в каждой алгебре из
- поляризованное многообразие алгебр и в каждой алгебре из  конгруэнции перестановочны, то мальцевское произведение
конгруэнции перестановочны, то мальцевское произведение 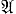
 ○
○ 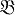 любых подмногообразий
любых подмногообразий 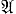 ,
, 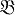 из
из  есть многообразие. В частности, можно говорить о группоиде GI (
есть многообразие. В частности, можно говорить о группоиде GI ( ) подмногообразий любого многообразия
) подмногообразий любого многообразия  групп, колец и т. п. Если
групп, колец и т. п. Если  - многообразие всех групп или всех алгебр Ли над фиксированным полем Р характеристики иуль, то GI (
- многообразие всех групп или всех алгебр Ли над фиксированным полем Р характеристики иуль, то GI ( ) - свободная полугруппа [1].
) - свободная полугруппа [1].
Лит. : [1] Мальцев А. И., Алгебраические системы, М., 1970; [2] Кон П., Универсальная алгебра, пер. с англ., М., 1968; [3] Нейман X., Многообразия групп, пер. с англ., М., 1969; [4] Биркгоф Г., Теория структур, пер. с англ., М., 1952; [5] Perkins P., «J. of Algebra», 1969, v. 11, № 2, p. 298-314; [6] Курский В. Л., «Докл. АН СССР», 1965, т. 163, №4, с. 815-18; [7] Jónsson В., «Math. Scand. », 1967, v. 21, № 1, p. 110-21; [8] Baker К. A., «Pacific J. of Math. », 1969, v. 28, № 1, p. 9-15; [9] Sсhwabauer R., «Рrос. Amer. Math. Soc. », 1969, v. 20, № 2, p. 503-04; [10] Baker K. A., «Trans. Amer. Math. Soc. », 1974, v. 190, p. 125-50.
Д. M. Смирнов.
Источники:
- Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'