
АЛГЕБРАИЧЕСКИХ СИСТЕМ КВАЗИМНОГООБРАЗИЕ
Расстановка ударений: АЛГЕБРАИ`ЧЕСКИХ СИСТЕ`М КВАЗИМНОГООБРА`ЗИЕ
АЛГЕБРАИЧЕСКИХ СИСТЕМ КВАЗИМНОГООБРАЗИЕ - класс алгебраич. систем (Ω-систем), аксиоматизируемый при помощи специальных формул логич. языка 1-й ступени, к-рые наз. квазитождествами, или условными тождествами, и имеют вид:
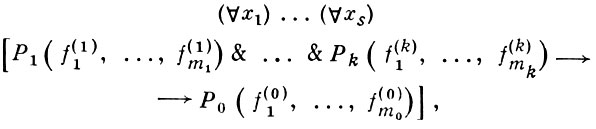
где 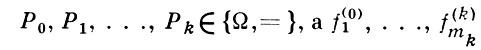 - термы сигнатуры Ω от предметных переменных x1, ..., xs . В силу теоремы Мальцева [1], А. с. к.
- термы сигнатуры Ω от предметных переменных x1, ..., xs . В силу теоремы Мальцева [1], А. с. к.  сигнатуры Ω может быть определено также как абстрактный класс Ω-систем, содержащий единичную Ω-систему Е и замкнутый относительно подсистем и фильтрованных произведений (см. [1], [2]). Аксиоматизируемый класс Ω-систем является квазимногообразием тогда и только тогда, когда он содержит единичную Ω-систему Е и замкнут относительно подсистем и декартовых произведений. Если
сигнатуры Ω может быть определено также как абстрактный класс Ω-систем, содержащий единичную Ω-систему Е и замкнутый относительно подсистем и фильтрованных произведений (см. [1], [2]). Аксиоматизируемый класс Ω-систем является квазимногообразием тогда и только тогда, когда он содержит единичную Ω-систему Е и замкнут относительно подсистем и декартовых произведений. Если  - квазимногообразие сигнатуры Q, то подкласс
- квазимногообразие сигнатуры Q, то подкласс  1 тех систем
1 тех систем  , которые изоморфно вложимы в подходящие системы из некоторого квазимногообразия
, которые изоморфно вложимы в подходящие системы из некоторого квазимногообразия  сигнатуры Ω ' ⊇ Ω, сам является квазимногообразием. Напр., класс полугрупп, вложимых в группы, есть квазимногообразие; класс ассоциативных колец без делителей нуля, вложимых в ассоциативные тела, также является квазимногообразием.
сигнатуры Ω ' ⊇ Ω, сам является квазимногообразием. Напр., класс полугрупп, вложимых в группы, есть квазимногообразие; класс ассоциативных колец без делителей нуля, вложимых в ассоциативные тела, также является квазимногообразием.
Квазимногообразие  сигнатуры Ω наз. конечно определимым (или обладающим конечным базисом квазитождеств), если существует такое конечное множество S квазитождеств сигнатуры Ω, что
сигнатуры Ω наз. конечно определимым (или обладающим конечным базисом квазитождеств), если существует такое конечное множество S квазитождеств сигнатуры Ω, что  состоит из тех и только тех Ω-систем, в к-рых истинны все формулы из множества S. Напр., квазимногообразие всех полугрупп с сокращением определяется двумя квазитождествами
состоит из тех и только тех Ω-систем, в к-рых истинны все формулы из множества S. Напр., квазимногообразие всех полугрупп с сокращением определяется двумя квазитождествами
zx = zy → х = у, xz = yz → x = у.
и потому конечно определимо. Напротив, квазимногообразие полугрупп, вложимых в группы, не имеет конечного базиса квазитождеств (см. [1], [2]).
Если  - произвольный (не обязательно абстрактный) класс Ω-систем, то наименьшее среди квазимногообразий, содержащих
- произвольный (не обязательно абстрактный) класс Ω-систем, то наименьшее среди квазимногообразий, содержащих  , наз. импликативным замыканием класса
, наз. импликативным замыканием класса  . Оно состоит из подсистем изоморфных копий фильтрованных произведений Ω-систем из класса
. Оно состоит из подсистем изоморфных копий фильтрованных произведений Ω-систем из класса  ∪ {E}, где Е - единичная Ω-система. Если
∪ {E}, где Е - единичная Ω-система. Если  - импликативное замыкание класса Ω-систем
- импликативное замыкание класса Ω-систем 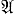 , то
, то 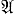 наз. порождающим классом квази многообразия
наз. порождающим классом квази многообразия  . Квазимногообразие
. Квазимногообразие  порождается одной системой тогда и только тогда, когда для любых двух систем А, В из
порождается одной системой тогда и только тогда, когда для любых двух систем А, В из  существует в классе
существует в классе  система С, содержащая подсистемы, изоморфные системам А, В (см. [1]). Всякое квазимногообразие
система С, содержащая подсистемы, изоморфные системам А, В (см. [1]). Всякое квазимногообразие  , содержащее неодноэлементную систему, обладает свободными системами любого ранга, к-рые являются одновременно свободными системами в эквациональном замыкании класса
, содержащее неодноэлементную систему, обладает свободными системами любого ранга, к-рые являются одновременно свободными системами в эквациональном замыкании класса  . Квазимногообразия Ω-систем, содержащиеся в к.-л. фиксированном квазимногообразии
. Квазимногообразия Ω-систем, содержащиеся в к.-л. фиксированном квазимногообразии  сигнатуры Ω, составляют полную решетку относительно теоретико-множественного включения. Атомы решетки всех квазимногообразий сигнатуры Ω наз. минимальными квазимногообразиями сигнатуры Ω. Минимальное квазимногообразие
сигнатуры Ω, составляют полную решетку относительно теоретико-множественного включения. Атомы решетки всех квазимногообразий сигнатуры Ω наз. минимальными квазимногообразиями сигнатуры Ω. Минимальное квазимногообразие 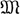 порождается любой своей неединичной системой. Каждое квазимногообразие
порождается любой своей неединичной системой. Каждое квазимногообразие  , обладающее неединичной системой, содержит хотя бы одно минимальное квазимногообразие. Если
, обладающее неединичной системой, содержит хотя бы одно минимальное квазимногообразие. Если  - квазимногообразие Ω-систем конечной сигнатуры Ω, то все его подквазимногообразия составляют группоид относительно мальцевского
- квазимногообразие Ω-систем конечной сигнатуры Ω, то все его подквазимногообразия составляют группоид относительно мальцевского  - умножения (см. [3]).
- умножения (см. [3]).
Лит. : [1] Мальцев А. И., Алгебраические системы, М., 1970; [2] Кон П., Универсальная алгебра, пер. с англ., М., 1968; [3] Мальцев А. И., «Сиб. матем. ж. », 1967, т. 8, № 2, с. 346-65.
Д. М. Смирнов.
Источники:
- Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'