АЛГЕБРАИЧЕСКИХ МНОГООБРАЗИЙ АРИФМЕТИКА

Расстановка ударений: АЛГЕБРАИ`ЧЕСКИХ МНОГООБРА`ЗИЙ АРИФМЕ`ТИКА

АЛГЕБРАИЧЕСКИХ МНОГООБРАЗИЙ АРИФМЕТИКА, арифметическая алгебраическая геометрия, - направление в алгебраич. геометрии, изучающее свойства алгебраич. многообразий, определенных над полями так наз. арифметического типа, т. е. конечными, локальными и глобальными полями алгебраич. чисел или алгебраич. функций. В случае конечных полей основным является изучение числа рациональных точек алгебраич. многообразия в этих полях и их конечных расширениях. Используемая для такого изучения дзета-функция многообразия оказала большое влияние на развитие методов алгебраич. геометрии. Большое значение имеют также оценки числа точек снизу (см. [1], [4]).

Если X - алгебраич. многообразие (или схема) над локальным полем К с полем вычетов k, то рассмотрение множества X(K) рациональных точек со значениями в К позволяет связать две совершенно различные задачи: нахождение решений сравнений (или точек многообразий над конечными полями) и целочисленных или рациональных решений диофантовых уравнений (см. Хассе принцип). Задавая многообразие X системой уравнений с коэффициентами из кольца А целых элементов поля К, можно определить редукцию этого многообразия той же системой уравнений, но с коэффициентами, взятыми по модулю максимального идеала кольца А. Получаются «многообразие» X₀ над полем вычетов k и канонич. отображение, или редукция:

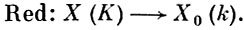
Приведенное описание редукции трудно объяснить в рамках классич. алгебраич. геометрии. Это явилось одной из причин введения понятия схем, на языке к-рых описанный процесс допускает строгое определение. Основная задача состоит в определении образа отображения Red, т. е. в нахождении тех точек х ∈ Х₀ (k), к-рые поднимаются до рациональных K-точек многообразия; Гензеля лемма утверждает, что это так, если х - неособая точка. Наиболее общие результаты об этом см. [4].

Другим кругом вопросов, относящихся к локальной А. м. а., является изучение форм над такими полями. Пусть F - форма от n переменных степени d над локальным полем; гипотеза Артина утверждает, что при n > d² уравнение F = 0 имеет нетривиальное решение. В функциональном случае справедливость этого утверждения известна. Для р-адических полей доказано, что для каждого d имеется такое конечное число простых A(d), что гипотеза Артина верна для форм степени d; если p ∉ A(d). В 1966 было показано, что уже множество A(L) не пусто, тем самым гипотеза Артина была опровергнута (см. [4]). Неизвестно (1977), верна ли она для форм нечетной степени.

А. м. а. над глобальными полями представляет собой наиболее обширную и разветвленную область алгебраич. геометрии. Сюда относятся диофантова геометрия, теория полей классов, теории дзета-функций многообразий, комплексное умножение абелевых функций (или многообразий). Все эти теории развиваются параллельным образом для числовых и функциональных полей. Впервые такая возможность была продемонстрирована развитием теории полей классов в 30-х гг. 20 в., она основана на глубокой аналогии между этими полями, получившей наиболее полное воплощение в конструкциях теории схем.

Лит. : [1] Боревич 3. И., Шафаревич И. Р., Теория чисел, 2 изд., М., 1972; [2] Вейль А., «Математика», 1958, т. 2, № 4; [3] Grothendieck A., DiеudоnnéJ., Eléments de géométrie algébrique I. В., 1971; [4] Итоги науки. Алгебра. Топология. Геометрия. 1970, М., 1971, с. 111-152; [5] Swinnerton-Dyer Н. P. F., в кн. : Proceedings of Symposia in pure mathematics, v. 20, 1969, Providence, 1971.

A. H. Паршин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.