АЛГЕБРАИЧЕСКИЙ ЦИКЛ

Расстановка ударений: АЛГЕБРАИ`ЧЕСКИЙ ЦИ`КЛ

АЛГЕБРАИЧЕСКИЙ ЦИКЛ на алгебраическом многообразии - элемент свободной абелевой группы, множество свободных образующих к-рой - все замкнутые неприводимые подмногообразия данного алгебраич. многообразия. Подгруппа группы С(х) алгебраич. циклов на многообразии А, порожденная подмногообразием коразмерности р, обозначается через С^p (Х). Группа С(X) представима в виде прямой суммы

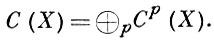
Подгруппа С¹ (X) совпадает с группой дивизоров Вейля на X.

В дальнейшем X обозначает неособое проективное алгебраич. многообразие размерности n над алгебраически замкнутым полем k. Если k-поле комплексных чисел 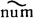, то каждый А. ц. Z ∈ C^p (X) определяет (2n - 2р)-мерный класс гомологий [Z] ∈ Н_{2n - 2p} (Х, ℤ) и, по двойственности Пуанкаре, класс когомологий γ (Z) ∈ Н^2p (X, ℤ). Классы гомологий (соответственно когомологий) вида [Z] (соответственно γ (Z)) наз. алгебраическими классами гомологий (соответственно когомологий). Каждый аналитич. цикл гомологичен А. ц. Имеется предположение (гипотеза Ходжа), что целочисленный {2n - 2р)-мерный цикл Г на X гомологичен А. ц. тогда и только тогда, когда интегралы всех замкнутых дифференциальных форм типа (2p - q, q), q ≠ p, по Г равны 0. Эта гипотеза доказана лишь в случаях р = 1 (для n = 2 см. [6], для всех n см. [7]) и р = n - 1, а также для отдельных классов многообразий (см. [4]).

Если W = ∑ n_i W_i А. ц. на произведении двух многообразий X × Т, то множество циклов на X вида

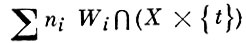
наз. семейством А. ц. на X, параметризованным базой Т. При этом обычно требуют, чтобы проекция каждого подмногообразия W_i на Т была плоским морфизмом. Если W = W_i определяется неприводимым подмногообразием, то соответствующее семейство А. ц. на X наз. семейством алгебраических подмногообразий. В частности, для любого плоского морфизма f: X → У алгебраич. многообразий его слои Х_y образуют семейство алгебраич. подмногообразий X, параметризованное базой Y. Другим частным случаем этого понятия являются линейные системы. Все члены семейства алгебраич. подмногообразий (соответственно алгебраич. циклов) проективного многообразия X, параметризованного связной базой, имеют одинаковый Гильберта многочлен (соответственно виртуальный арифметический род).

А. ц. Z и Z' на многообразии X наз. алгебраически эквивалентными (что обозначается Z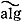Z'), если они принадлежат одному и тому же семейству, параметризованному связной базой. Интуитивно эквивалентность А. ц. означает, что Z можно алгебраически деформировать в Z'. Если в этом определении требовать, чтобы в качестве базы Т можно было выбрать рациональное многообразие, то А. ц. Z и Z' наз. рационально эквивалентными (что обозначается Z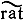Z'). В случае, когда Z, Z' ∈ С¹ (Х), понятие рациональной эквивалентности сводится к понятию линейной эквивалентности дивизоров. Подгруппа А. ц., рационально (соответственно алгебраически) эквивалентных нулю, обозначается C_rat (X) (соответственно C_alg (X)). Каждая из этих групп является прямой суммой своих компонент:

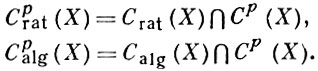
Факторгруппа С¹ (X)/C¹_alg (X) конечно порождена и наз. группой Нерона-Севери многообразия X. Вопрос о конечной порожденности при р > 1 фактор-группы С^p (X)/C^p_alg (X) остается открытым (1977). Факторгруппа C¹_alg (X)/C¹_rat (X) обладает структурой абелева многообразия (см. Пикара схема). Операция пересечения циклов позволяет определить умножение в факторгруппе C(X)/C_rat (X), превращающее ее в коммутативное кольцо, наз. кольцом Чжоу многообразия X (см. Пересечений теория).

Для любой теории когомологий Вейля Н*(X) существует однозначно определенный гомоморфизм групп

А. ц. Z и Z' наз. гомологически эквивалентными (что обозначается Z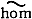Z'), если γ (Z) = = γ (Z'). Подгруппа А. ц., гомологически эквивалентных нулю, обозначается C_hom (X). Имеет место вложение C_alg (X) ⊂ C_hom (X). Факторгруппа C(X)/C_hom (X) конечно порождена и является подкольцом в кольце Н*(X), к-рое обозначается через А*(X) и наз. кольцом алгебраических классов когомологий Вейля. Неизвестно (1977), зависит ли А*(X) от выбранной теории когомологий Вейля.

А. ц. Z и Z' наз. τ-эквивалентными (что обозначается Z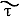Z'), если существует m ≥ 1 такое, что mZ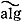mZ'. Подгруппа А. ц., τ-эквивалентных нулю, обозначается через С_τ (X). А. ц. Z и Z' из С^p (X) наз. численно эквивалентными (что обозначается Z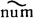Z'), если для любого W ∈ C^{n - p} (X) имеет место равенство WZ = WZ', при условии, что обе части равенства определены. Подгруппа А. ц., численно эквивалентных нулю, обозначается через C_num (X). Имеют место включения

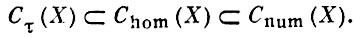
Для дивизоров группы С_τ (Х) ∩ С¹ (Х), C_hom (X) ∩ С¹ (X) и С_num (Х) ∩ С¹ (Х) совпадают [6]. Однако (как показывает построенный в [5] для случая k = С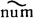 контрпример)

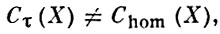
где C_hom (X) рассматривается относительно обычной теории когомологий с рациональными коэффициентами. Аналогичный контрпример построен для поля k произвольной характеристики и l-адической теории когомологий Вейля. Остается открытым (1977) вопрос о совпадении групп С_hom (X) и C_num (X).

Пусть X вложено в проективное пространство и L_X - класс когомологий гиперплоского сечения. Алгебраич. класс когомологий

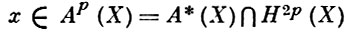
наз. примитивным, если L^{n - p}_X = 0. В случае, когда k есть поле комплексных чисел 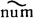, билинейная форма

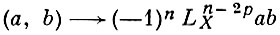
положительно определена на подпространстве примитивных классов в А^p (X). Аналогичное утверждение для произвольного k, тесно связанное с гипотезами Вейля о дзета-функции на алгебраич. многообразии, доказано лишь для n ≤ 2.

Если многообразие X определено над полем k, не являющимся алгебраически замкнутым полем, то группа Галуа сепарабельного алгебраич. замыкания G(k/k) поля k действует на когомологиях Вейля H*(X¯), где X¯ = X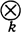k. Каждый элемент из А*(X) инвариантен относительно нек-рой подгруппы конечного индекса группы G(k/k). Имеется предположение (гипотеза Тейта об алгебраических циклах), что обратное утверждение также справедливо, если k конечно порождено над своим простым подполем. На этом предположении основаны многие гипотезы о дзета-функции алгебраич. многообразия [2].

Лит. : [1] Бальдассари М., Алгебраические многообразия, пер. с англ., М., 1961; [2] Тэйт Дж., «Успехи матем. наук», 1965, т. 20, в. 6, с. 27-40, пер. с англ. ; [3] Итоги науки и техники. Алгебра. Топология. Геометрия, т. 12, М., 1974, 77-170; [4] Кleiman S. L., в сб. : Dix exposés sur cohomologie des schémas, Amst. - P., 1968, p. 359-86; [5] Griffiths P. A., «Ann. Math. », 1969, v. 90, Л» 3, p. 496-541; [6] Lefschetz S., L'Analysis situs et la géometrie algébrique, P., [1924]; [7] Hоdge W., The theory and applications of harmonic integrals, Camb., 1941; [8] Groupes de monodromie en géométrie algébrique, В., 1973.

И. В. Долгачев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.