
АЛГЕБРАИЧЕСКИЙ МНОГОЧЛЕН НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ
Расстановка ударений: АЛГЕБРАИ`ЧЕСКИЙ МНОГОЧЛЕ`Н НАИЛУ`ЧШЕГО ПРИБЛИЖЕ`НИЯ
АЛГЕБРАИЧЕСКИЙ МНОГОЧЛЕН НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ - многочлен, наименее уклоняющийся от заданной функции. Точнее, пусть измеримая функция f(x) интегрируема с р-й степенью (р ≥ 1) на [а, b] и Нn - множество алгебраич. многочленов степени не выше n. Величину
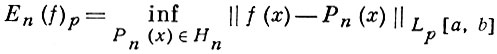
(*)
наз. наилучшим приближением, а многочлен, для к-рого нижняя грань достигается, наз. алгебраическим многочленом наилучшего приближения в Lp [a, b]. Многочлены, наименее уклоняющиеся от данной непрерывной функции в равномерной (р = ∞) метрике, впервые встретились (1852) у П. Л. Чебышева и были исследованы им в 1856 (см. [1]). Доказательство существования А. м. н. п. дано Э. Борелем [2]. П. Л. Чебышев показал, что Р0n (х) является А. м. н. п. в равномерной метрике тогда и только тогда, когда у разности f(x) - Р0n (х) существует чебышевский альтернанс; в этом случае такой многочлен единствен. При р > 1 А. м. н. п. единствен в силу строгой выпуклости пространства Lp . При р = 1 единственности нет, но для непрерывных функций единственность А. м. н. п. доказана Д. Джексоном [3]). Скорость стремления Еn (f)p к нулю оценивается в Джексона теореме.
Аналогично (*) определяется А. м. н. п. для большого числа m переменных. Если число переменных m ≥ 2, то А. м. н. п. (в равномерной метрике), вообще говоря, не единствен.
Лит. : [1] Чебышев П. Л., Полное собрание сочинений, т. 2, М., 1947, с. 478, с. 152-236; [2] Воrеl Е., Lecons sur les fonctions de variables réelles et les développements en série de polynomes, P., 1905; [3] Jасksоn D., «Amer. J. Math. », 1924, v. 46; [4] Гapкави А. Л., в кн. : Итоги науки. Математический анализ. 1967, М., 1969.
Ю. Н. Субботин
Источники:
- Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'