
АЛГЕБРАИЧЕСКАЯ ФУНКЦИЯ
Расстановка ударений: АЛГЕБРАИ`ЧЕСКАЯ ФУ`НКЦИЯ
АЛГЕБРАИЧЕСКАЯ ФУНКЦИЯ - функция у = f(x1, ..., xn) переменных x1, ..., xn, удовлетворяющая уравнению

(1)
где F - неприводимый многочлен от у, x1, ..., xn с коэффициентами из нек-рого поля K, наз. полем констант. А. ф., заданная над этим полем, наз. А. ф. над полем K. Многочлен F(y, x1, ..., xn) часто записывается по степеням переменного у, так что уравнение (1) приобретает вид
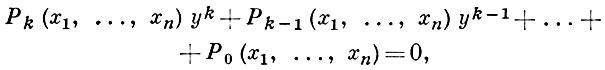
где Pk (x1, ..., xn), ..., P0 (x1, ..., xn) - многочлены от x1, ..., xn, причем Рk (x1, ..., xn) ≠ 0. Число k - степень многочлена F относительно у, наз. степенью А. ф. В случае k = 1 А. ф. может быть представлена в виде отношения
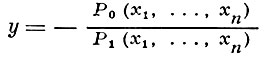
многочленов и наз. рациональной функцией от x1, ..., xn . При k = 2, 3, 4 А. ф. может быть выражена через квадратные и кубич. радикалы от рациональных функций переменных x1, ..., xn ; при k > 4 это, вообще говоря, невозможно.
Исторически сложилось три подхода к теории А. ф. : теоретико-функциональный, возникновение к-рого связано в первую очередь с работами Н. Абеля (N. Abel), К. Вейерштрасса (К. Weierstrass) и Б. Римана (В. Riemann), арифметико-алгебраический, восходящий к Р. Дедекинду (R. Dedekind), Г. Веберу (Н. Weber) и К. Гензелю (К. Hensel) и алгебро-геометрический, берущий свое начало от работ А. Клебша (A. Clebsh), М. Нётера (М. Noether) и др. (см. Алгебраическая геометрия). Первое направление в теории А. ф. одного переменного связано с изучением А. ф. над полем комплексных чисел и рассмотрением их как мероморфных функций на римановых поверхностях и комплексных многообразиях; важнейшие применяемые здесь методы-геометрич. и топологич. методы теории аналитич. функций. Арифметико-алгебраич. подход связан с изучением А. ф. над произвольными полями. Применяемые методы - чисто алгебраические. Особенно большое значение имеют теории нормирований и расширений полей. При алгебро-геометрич. подходе А. ф. рассматриваются как рациональные функции на алгебраич. многообразии, а их изучение ведется методами алгебраич. геометрии. Первоначально эти подходы различались не только по методам и по способу изложения, но и по терминологии. На современном этапе такое разделение направлений представляется в значительной мере условным, ибо в функциональном направлении широко используются алгебраич. методы, а многие результаты, полученные в первом направлении с помощью теоретико-функциональных и топологич. методов, успешно переносятся на случай более общих полей при помощи алгебраич. аналогов функциональных и топологич. методов.
Алгебраические функции одного переменного. Над полем С комплексных чисел А. ф. одного переменного y = f(х) [B упрощенной записи - у(х)] является k-значной аналитич. функцией. Если обозначить через D(х) дискриминант многочлена
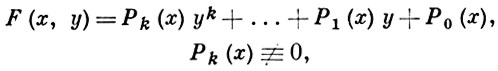
(2)
(т. е. многочлена, для к-рого F(x, f(х)) = 0), получающийся исключением у из уравнений
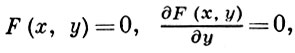
и составить уравнение
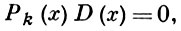
то корни x1, ..., xm этого последнего уравнения наз. критическими значениями А. ф. y = f(x). Дополнительное множество G = C - {x1, ..., xm} наз. некритическим множеством. Для любой точки x0 ∈ G уравнение (2) имеет k различных корней x01, ..., x0k, причем выполняются условия
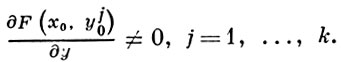
По теореме о неявных функциях, в окрестности точки х0 существует k однозначных аналитич. функций f01 (x), ..., f0k (x), удовлетворяющих условиям
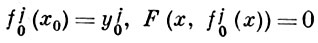
и разлагающихся в сходящиеся ряды
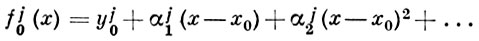
(3)
Таким образом, для каждой точки x0 ∈ G строится k элементов аналитич. функций, наз. функциональными элементами с центром в точке х0 . Для любых двух точек х1, x2 ∈ G любые элементы f1i (x) и f2j (х) с центрами, соответственно, х1 и х2, получаются друг из друга аналитич. продолжением вдоль нек-рой кривой, лежащей в G; в частности, таким способом связаны и любые два элемента с одним центром. Если х0 - критич. точка А. ф., то возможны два случая: 1) х0 - корень дискриминанта, т. е. D(x0) = 0, но Pk (x0) ≠ 0; 2) Pk (x0) = 0.
Случай 1. Пусть K0 - малый круг с центром в х0, не содержащий других критич. точек, a f'1 (x), ..., f'n (x) - система регулярных элементов с центром в х' ∈ К0 0, х' ≠ х0 . Эти функции остаются ограниченными при х' → х0 . Пусть, далее, D - окружность с центром х0, проходящая черех х'; она целиком лежит внутри K0 . Аналитич. продолжение нек-рого элемента, напр. | f'1 (x), вдоль окружности D (скажем, обходя х0 по часовой стрелке) приводит к элементу f'(х), также принадлежащему системе элементов с центром х'. Эта система состоит из k элементов, и нек-рое (минимальное) конечное число а1 ≤ k таких обходов приводит к исходному элементу f'1 (x). Получается подсистема f'1 (x), ..., f'a1 (x) элементов с центром х'; каждый из этих элементов может быть получен аналитическим продолжением другого путем обходов вокруг точки х0 ; такая подсистема наз. циклом. Вся система f'1 (x), ..., f'k (x) разбивается на нек-рое число непересекающихся циклов
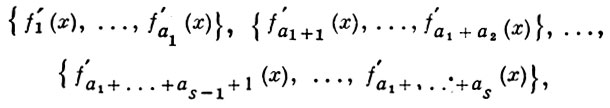
a1 + a2 + ... + as - 1 + as = k. Элемент f'1 (x) не является (в случае а1 > 1) однозначной функцией от х в круге K0, но будет однозначной аналитич. функцией от параметра 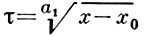 в окрестности точки τ = 0. В нек-рой окрестности этой точки элементы f'1 (x), ..., f'a1 (x) первого цикла представимы в виде сходящихся рядов
в окрестности точки τ = 0. В нек-рой окрестности этой точки элементы f'1 (x), ..., f'a1 (x) первого цикла представимы в виде сходящихся рядов
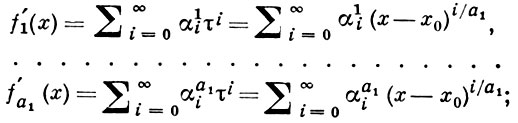
(4)
аналогичные разложения имеют место для элементов других циклов. Такие разложения элементов по дробным степеням разности х - х0, где х0 - критич. точка, наз. рядами Пюизё. Преобразованием τ → τ t, r = e2π i/a, соответствующим однократному обходу вокруг х0, ряды Пюизё элементов одного цикла переводятся друг в друга в циклич. порядке, т. е. происходит циклич. перестановка рядов и соответствующих элементов. Обходам вокруг критич. точки соответствуют перестановки элементов с центром в этой точке; эти перестановки состоят из циклов порядков а1, ..., as, ∑ ai = k. Определяемые таким способом подстановки составляют группу монодромии А. ф. Если хотя бы одно из аi больше 1, критич. точка х0 наз. алгебраической точкой ветвления А. ф. ; числа аi (иногда аi - 1) наз. индексами (или порядками) ветвления А. ф.
Случай 2. Заменой функции у на Рk (х)у сводится к 1); получаются разложения, аналогичные разложениям (4), к-рые могут содержать конечное число членов с отрицательными показателями:
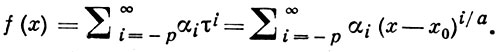
(5)
При р > 0 точка х0 является полюсом порядка р А. ф. Обычно А. ф. рассматриваются на сфере Римана S, т. е. на комплексной плоскости, пополненной бесконечно удаленной точкой х = ∞. Введение переменной τ = 1/x сводит этот случай к предыдущему; в окрестности точки τ = 0 (х = ∞) имеет место разложение
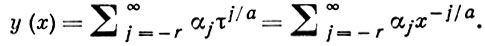
(6)
При r > 0 точка х = ∞ является полюсом порядка r.
Параметр разложения в рядах (3), (4), (5), (6) наз. локальной униформизующей для А. ф. Если х0 - некритич. точка А. ф., таким параметром может быть τ = х - x0 ; если же x0 - критич. точка, за параметр может быть принят корень 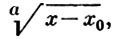 , где а - натуральное число. Совокупность всех описанных выше элементов А. ф. образует полную А. ф. в смысле Вейерштрасса. А. ф. не имеют других особенностей, кроме, быть может, алгебраич. точек ветвления и полюсов. Верно и обратное: функция y = f(x), аналитическая и не более чем s-значная во всех точках сферы Римана, за исключением конечного числа точек х1, ..., хm и х = ∞, а в этих точках имеющая лишь полюсы или алгебраич. точки ветвления, есть А. ф. степени k ≤ s.
, где а - натуральное число. Совокупность всех описанных выше элементов А. ф. образует полную А. ф. в смысле Вейерштрасса. А. ф. не имеют других особенностей, кроме, быть может, алгебраич. точек ветвления и полюсов. Верно и обратное: функция y = f(x), аналитическая и не более чем s-значная во всех точках сферы Римана, за исключением конечного числа точек х1, ..., хm и х = ∞, а в этих точках имеющая лишь полюсы или алгебраич. точки ветвления, есть А. ф. степени k ≤ s.
Риманова поверхность полной А. ф. компактна и является k-листным накрытием сферы Римана, точками разветвления к-рого являются, быть может, критич. точки и точка х = ∞. А. ф. представляют собой единственный класс функций, риманова поверхность к-рых компактна. Род римановой поверхности А. ф. играет важную роль; он наз. родом А. ф. Он вычисляется по Римана-Гурвица формуле. Род рациональной функции равен 0; ее риманова поверхность есть сфера Римана. Риманова поверхность эллиптич. функций, удовлетворяющих уравнениям 3-й и 4-й степеней, есть тор; род этих функций равен 1.
Универсальная накрывающая римановой поверхности А. ф. является односвязным двумерным многообразием, т. е. имеет тривиальную фундаментальную группу и конформно эквивалентна либо сфере Римана, либо комплексной плоскости, либо внутренности единичного круга. В первом случае А. ф. является рациональной, во втором - эллиптич. функцией; третий случай является общим.
С теорией римановых поверхностей А. ф. тесно связана проблема униформизации А. ф. Функция у = f(х) может быть униформизована, если у и х представимы как однозначные аналитич. функции
y = y(t), x = x(t)
параметра t, тождественно удовлетворяющие уравнению (2). Локально проблема униформизации решается при помощи локальной униформизующей; однако интерес представляет ее решение «в целом». При k = 1, т. е. когда у(х) есть рациональная функция от х, за этот параметр может быть принято переменное х - x0 ; при k = 2 униформизация достигается посредством рациональных или тригонометрич. функций. Напр., если у(х) удовлетворяет уравнению
y2 - x2 = 1,
то можно положить
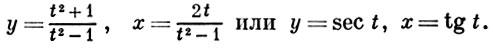
При k = 3, 4, в случае А. ф. рода 1, униформизация достигается посредством эллиптических функций. Наконец, при k > 4, в случае А. ф. рода > 1, униформизация осуществляется при помощи автоморфных функций.
Алгебраические функции многих переменных. Если f - А. ф. от переменных x1, ..., xn, то множество всех рациональных функций R(у, x1, ..., xn) образует поле Kf, совпадающее с полем рациональных функций на алгебраич. гиперповерхности в пространстве (n + 1) измерений, задаваемой уравнением F (у, x1, ..., xn) = 0. Если поле констант k есть поле комплексных чисел С, а n = 1, то поле Kf совпадает с полем мероморфных функций на римановой поверхности А. ф. f. Поле Kf является расширением конечного типа поля констант k степени трансцендентности n (см. Расширение поля). В частности, любые n + 1 элементов этого поля связаны алгебраич. уравнением и тем самым каждый из них определяет А. ф. от остальных элементов. Любое расширение K конечного типа поля k степени трансцендентности n наз. полем алгебраических функций от n переменных (иногда функциональным полем). Каждое такое поле содержит чисто трансцендентное расширение k(x1, ..., xn) поля k (называемое полем рациональных функций от n переменных). Любой элемент у ∈ K удовлетворяет нек-рому алгебраич. уравнению Ф(у, x1, ..., xn) = 0 и может рассматриваться как А. ф. от переменных x1, ..., xn . Каждое поле K А. ф. от n переменных изоморфно полю рациональных функций на нек-ром алгебраическом многообразии размерности n, называемом моделью поля K. Если поле констант k является алгебраически замкнутым полем характеристики 0, то каждое поле А. ф. имеет неособую проективную модель (см. Разрешение особенностей). Пусть S - множество всех нетривиальных нормирований поля А. ф. K, неотрицательных на поле констант. Снабженное естественной топологией, оно наз. абстрактной римановой поверхностью поля K [1]. В случае полей А. ф. от одной переменной риманова поверхность совпадает с множеством неособой проективной модели, к-рая в этом случае определена однозначно с точностью до изоморфизма. Многие понятия и результаты алгебраич. геометрии модели поля K можно переформулировать на языке теории нормирований поля (см. [1], [6]). Особенно близкая аналогия существует для полей А. ф. одного переменного, теория к-рых фактически совпадает с теорией алгебраич. кривых.
Каждое поле А. ф. от одного переменного является полем частных дедекиндова кольца, - благодаря этому многие результаты и понятия теории делимости в полях алгебраич. чисел переносятся на случай функциональных полей [12]. Многие задачи и построения в теории алгебраич. чисел служат мотивировкой для аналогичных задач и построений в полях А. ф., и наоборот. Так, напр., перенос разложения Пюизё в теорию алгебраич. чисел привел к созданию К. Гензелем р-адического метода в теории чисел. Теория полей классов, первоначально относящаяся к алгебраич. числам, была позже перенесена на функциональный случай (см. [2]). Особенно близкая аналогия существует между полями алгебраич. чисел и полями А. ф. над конечным полем констант. Напр., для последних определяется понятие дзета-функции и доказывается аналог гипотезы Римана (см. Дзета-функция в алгебраической геометрии).
Лит. : [1] Зарисский О., Самюэль П., Коммутативная алгебра, пер. с англ., т. 1-2, М., 1963; [2] Серр Ж.-П., Алгебраические группы и поля классов, пер. с франц., М., 1968; [3] Стоилов С, Теория функций комплексного переменного, пер. с рум., т. 1-2, М., 1962; [4] Чеботарёв Н. Г., Теория алгебраических функций, М. - Л., 1948; [5] Шафаревич И. Р., Основы алгебраической геометрии, М., 1972; [6] Шевалле К., Введение в теорию алгебраических функций от одной переменной, пер. с англ., М., 1959; [7] Арреll Р., Coursat Е., Théorie des fonctions algébriques, t. 1-2, P., 1929-30; [8] Dedekind R., Weber H., «J. reine und angew. Math. », 1879, Bd 92, S. 181-290; [9] Hensel K., Landsberg G., Theorie der algebraischen Funktionen einer Variabeln und ihre Anwendung auf algebraischen Kurven und Abelsche Integrale, Lpz., 1902; [10] Piсard E., Simart G., Théorie des fonctions algebriques de deux variables independents, t. 1-2, P., 1897, 1906; [11] Jung H. W. E., Einführung in die Theorie der algebraischen Funktionen zweier Veränderlicher, В., 1951; [12] Hasse H., Zahlentheorie, 2 Aufl., В., 1963; [13] Lang S., Algebraic functions, N. Y. - Amst., 1965.
А. Б. Жижченко.
Источники:
- Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'