
АЛГЕБРАИЧЕСКАЯ ТЕОРИЯ ЧИСЕЛ
Расстановка ударений: АЛГЕБРАИ`ЧЕСКАЯ ТЕО`РИЯ ЧИ`СЕЛ
АЛГЕБРАИЧЕСКАЯ ТЕОРИЯ ЧИСЕЛ - раздел теории чисел, основной задачей к-рого является изучение свойств целых чисел полей К алгебраических чисел конечной степени над полем ℚ рациональных чисел. Все целые числа поля К/ℚ - расширения К поля ℚ степени n - могут быть получены с помощью фундаментального базиса (ω1, ..., ωn), если в линейной форме x1 ω1, ..., xn ωn каждое xi пробегает все целые рациональные числа. При этом такое представление для каждого целого числа из К единственно.
Переход от целых рациональных чисел к целым алгебраическим не сопровождается ожидаемыми аналогиями. Первое нарушение аналогии относится к единицам. В то время как поле рациональных чисел имеет только две единицы: + 1 и - 1, в общих полях алгебраич. чисел может быть даже бесконечно много единиц. Пусть, напр., имеется вещественное квадратичное поле ℚ (√D)), где D > 1 - целое рациональное число, не равное точному квадрату. Его фундаментальный базис имеет вид (1, √D), D ≠ 1(mod 4). У двучленного Пелля уравнения х2 - Dy2 = 1 бесконечно много целочленных решений (х, y). Любое из них порождает единицу x + y√D поля ℚ (√D). Именно,
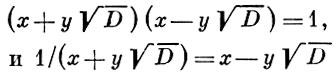
тоже является целым числом поля ℚ (√D). Единицы этого поля образуют бесконечную мультипликативную группу (группу единиц Пелля). Возникает вопрос о том, как устроена эта группа.
Второе нарушение аналогии, при переходе от поля рациональных чисел к полю алгебраич. чисел, связано с теоремой об однозначном разложении целых рациональных n на простые множители:
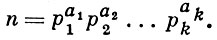
Для алгебраич. чисел это уже не так. Пусть, напр.,. имеется поле ℚ (√- 5); в нем число 6 можно разложить двумя существенно различными способами: 6 = 2*3, 6 = (1 + √- 5)(1 - √- 5). При переходе к полям более высокой степени картина усложняется. Возникает вопрос: что происходит с теоремой об однозначном разложении и имеет ли она вообще смысл в полях алгебраич. чисел.
Третье нарушение аналогий доставляют простые числа. При переходе к полям алгебраич. чисел они, вообще говоря, перестают быть простыми. Так, простое число 5 в поле гауссовых чисел ℚ (√- 1) распадается на два: 5 = (2 + √- 1) (2 - √- 1). Но в этом же поле число 7 остается простым. Возникает вопрос: существуют ли общие законы, управляющие поведением простых чисел при переходе к полям алгебраич. чисел более высокой степени. Другими словами, можно ли найти правила, к-рые давали бы однозначный ответ на вопрос - остается данное простое число простым при переходе к полю К/ℚ или распадается в нем, и если распадается, то на сколько множителей.
И наконец, последний (четвертый) вопрос касается общей структуры полей алгебраич. чисел. Поле ℚ является минимальным полем с нулевой характеристикой и не содержит собственных подполей. Любое другое поле алгебраич. чисел уже имеет подполя. Так, ℚ служит подполем любого поля алгебраич. чисел. Возникает вопрос: сколько подполей содержит данное поле К/ℚ - конечное или бесконечное - и как они устроены.
Эти четыре вопроса являются главными в А. т. ч., и ответы на них составляют ее содержание. Естественно начать рассмотрение с четвертого вопроса, так как ответ на него прольет свет и на первые три. Соответствующая задача была решена Э. Галуа (Е. Galois) в 20-х гг. 19 в. (см. Галуа теория). Конечность числа подполей расширения К/ℚ степени n над ℚ следует из существования взаимно однозначного соответствия (основного соответствия Галуа) между всеми подполями поля К и всеми подгруппами его группы Галуа, порядок (число элементов) к-рой конечен (и не превосходит n!).
Строение группы единиц поля было выяснено П. Дирихле (P. Dirichlet). Основную идею можно проследить на примере группы единиц Пелля (см. выше). Любая степень такой единицы (как положительная, так и отрицательная) будет единицей. Существует основная единица η = х0 + у0 √D, а все остальные являются ее целыми степенями, т. е. единицы Пелля составляют бесконечную циклич. группу с одной образующей. Этот факт есть частный случай общей теоремы Дирихле о единицах поля алгебраич. чисел: если поле К/ℚ имеет степень n = r1 + 2r2, где r1 - число вещественных, а r2 - число пар комплексно сопряженных полей для К/ℚ, то бесконечная группа единиц поля К/ℚ имеет r = r1 + r2 - 1 образующих единиц η1, ..., ηr, а все остальные являются произведениями их целочисленных степеней ηn11 ... ηnrr . Таким образом, бесконечная группа единиц поля К/ℚ является произведением r бесконечных циклич. подгрупп. Если домножить ее на конечную циклич. подгруппу корней из единицы, к-рые могут быть в К/ℚ, то будет получена самая общая картина строения группы единиц поля. Норма любой единицы поля, т. е. произведение этой единицы и всех ей сопряженных, равна единице поля ℚ.
Проблема неоднозначного разложения целых чисел в алгебраич. полях была решена Э. Куммером (Е. Kummer), к-рый, как и Э. Галуа, начал с частной задачи - попытки доказать великую теорему Ферма о невозможности решить в целых числах уравнение xp + yp = zp для любого простого р > 2. Э. Куммер разложил левую часть по корням р-й степени из 1, и задача была сведена к целым числам поля ℚ (ζ). Если бы для них существовало однозначное разложение на простые множители в поле ℚ (ζ), то достаточно было бы показать, что не все простые множители левой части имеют степень, кратную р. Вначале Э. Куммер так и считал, но П. Дирихле обратил его внимание на отсутствие однозначности. Именно для преодоления этой трудности Э. Куммер ввел идеальные числа, и это преобразило в дальнейшем все здание А. т. ч. Понятие идеального числа происходит из того, что если в поле k нет простых чисел, на к-рые однозначно распадалось бы любое целое число из k, то найдется другое поле К/k конечной степени над k, в к-ром существует необходимое количество чисел, играющих роль простых для поля k. Эти числа Э. Куммер назвал идеальными (так как они не принадлежат исходному полю k). С привлечением идеальных чисел теорема об однозначности разложения в поле к восстанавливается. При этом два числа поля, отличающиеся только единицей Дирихле (так наз. ассоциированные числа), имеют одни и те же идеальные множители. Понятие идеального числа относительно - для другого поля k' строится поле К'/k' другой степени над k', в к-ром содержатся идеальные числа поля k'.
Э. Куммер ввел также понятие класса идеальных чисел: два идеальных числа принадлежат одному классу, если их отношение лежит в первоначальном поле к. Он получил важный результат: число этих классов h конечно, и они образуют абелеву группу по умножению. Таким образом, любое идеальное число можно считать корнем h-й степени из нек-рого числа первоначального поля k. Число классов h явно выписывается через константы поля (регулятор, дискриминант, степень поля n).
В дальнейшем понятие идеального числа было заменено эквивалентным понятием идеала, к-рое удается описать средствами самого поля k, и уже в сер. 20 в. идеал уступил место более емкому понятию дивизор. Поэтому современная теория Куммера излагается на языке дивизоров. Но для полей алгебраич. чисел классич. понятие идеала совпадает с понятием дивизора. Далее всюду идет речь лишь о таких полях. Понятие идеала тесно связано с понятием неассоциированных чисел, что способствует пониманию глубоких связей теории Куммера и теории единиц Дирихле. Хотя Э. Куммеру и не удалось решить проблему Ферма, но его идеи вышли далеко за рамки этой задачи, и понятие идеала ныне является одним из главных для всей математики.
В связи с относительностью понятия простого идеального числа, или, в современной терминологии, простого идеала, третий вопрос о распадении простых чисел поля ℚ при переходе к полям алгебраич. чисел может быть поставлен в общем виде. Пусть дано поле k и его простой идеал 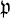 . Ставится вопрос о том, остается ли идеал простым при переходе от поля к к его расширению K = k(θ) или распадается в произведение простых идеалов поля К, и если распадается, то по какому закону. Этот вопрос приводит к полей классов теории - центральной части всей современной А. т. ч. Первое решение этого вопроса было дано Э. Куммером, показавшим, что если θ - корень неприводимого многочлена f(x), то простой идеал
. Ставится вопрос о том, остается ли идеал простым при переходе от поля к к его расширению K = k(θ) или распадается в произведение простых идеалов поля К, и если распадается, то по какому закону. Этот вопрос приводит к полей классов теории - центральной части всей современной А. т. ч. Первое решение этого вопроса было дано Э. Куммером, показавшим, что если θ - корень неприводимого многочлена f(x), то простой идеал 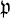 распадается в k(θ) по тому же закону, что и f(x) при переходе к полю вычетов (mod
распадается в k(θ) по тому же закону, что и f(x) при переходе к полю вычетов (mod 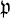 ). Другими словами, разложение
). Другими словами, разложение 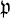 в k(θ) определяется сравнением
в k(θ) определяется сравнением
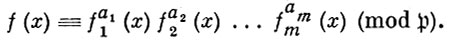
Параллельное равенство наз. формулой (или разложением) Куммера:
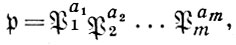
где  i - простые идеалы поля K = k(θ).
i - простые идеалы поля K = k(θ).
Это равенство в принципе решает третью задачу А. т. ч., но оно локально в том смысле, что требует проверки каждого простого идеала в отдельности. Задача же о разбиении всех простых идеалов на классы так, чтобы в одном классе закон разложения был один и тот же и чтобы, кроме того, можно было найти простые правила задания этих классов, решается теорией полей классов для расширения К/k с абелевой группой Галуа G(K/k).
Предварительное понятие класса можно получить из равенства (1). Пусть n - степень поля K/k, fi - относительная степень идеала βi . Вычисление относительной нормы NK/k обеих частей (1) приводит к равенству
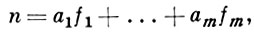
(2)
где ai, fi - натуральные. При фиксированном n уравнение (2) имеет конечное число решений, так что все простые идеалы поля к можно разбить на конечное число классов и собрать в один класс те из них, разложению Куммера к-рых соответствует один и тот же набор пар (аi, fi) из решения (2). Интерес представляют лишь бесконечные классы, поэтому можно оставить в стороне те классы, где имеется аi ≥ 2. Число простых идеалов с таким свойством конечно, и все они являются делителями дискриминанта 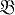 поля К/k.
поля К/k.
Для упрощения задачи поле К/k считается нормальным. В таких полях выполняется условие
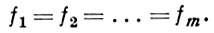
Поэтому все 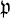 ×
× 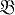 разбиваются на d(n) классов, где d(n) - функция числа делителей. Особый интерес представляет класс с условием m = n, где
разбиваются на d(n) классов, где d(n) - функция числа делителей. Особый интерес представляет класс с условием m = n, где

в нем 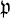 имеет максимальное число простых делителей поля К/k:
имеет максимальное число простых делителей поля К/k:
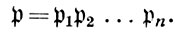
(3)
Такие 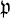 наз. вполне разложимыми, а их класс наз. главным классом поля k относительно К/k. В теории полей классов он является основным объектом изучения. Определение главного класса с помощью (3) требует доказательства того, что в поле k такие идеалы на самом деле существуют и что их бесконечно много. Поэтому основная задача теории полей классов состоит в том, чтобы определить главный класс средствами самого поля k, из к-рого бы следовала его бесконечность. Эта задача полностью решена для абелевых расширений К/k.
наз. вполне разложимыми, а их класс наз. главным классом поля k относительно К/k. В теории полей классов он является основным объектом изучения. Определение главного класса с помощью (3) требует доказательства того, что в поле k такие идеалы на самом деле существуют и что их бесконечно много. Поэтому основная задача теории полей классов состоит в том, чтобы определить главный класс средствами самого поля k, из к-рого бы следовала его бесконечность. Эта задача полностью решена для абелевых расширений К/k.
Для более подробного ознакомления с идеями теории полей классов необходимо общее понятие группы классов идеалов. Приведенное выше определение Куммера соответствует современному понятию абсолютной группы классов идеалов. Современные общие понятия группы классов принадлежат Г. Веберу (Н. Weber) и Т. Такаги (Т. Takagi) (см. [5]).
Г. Вебером введено понятие ведущего модуля группы классов. Пусть  - целый идеал поля k, L
- целый идеал поля k, L - подгруппа главных идеалов α поля k, заданных сравнением α ≡ 1 (mod
- подгруппа главных идеалов α поля k, заданных сравнением α ≡ 1 (mod  ), A
), A - подгруппа всех идеалов поля k, взаимно простых с
- подгруппа всех идеалов поля k, взаимно простых с  . Любая подгруппа H
. Любая подгруппа H с условием L
с условием L ⊆ H
⊆ H ⊆ A
⊆ A может быть объявлена главной, таким образом и будет построена группа классов A
может быть объявлена главной, таким образом и будет построена группа классов A /H
/H . При
. При  = 1 и H1 = L1 получается определение Куммера. В общем случае H
= 1 и H1 = L1 получается определение Куммера. В общем случае H состоит из прогрессий (mod
состоит из прогрессий (mod  ), вычеты к-рых образуют подгруппу всей мультипликативной группы (mod
), вычеты к-рых образуют подгруппу всей мультипликативной группы (mod  ). Порядок h
). Порядок h этой общей группы классов лежит в пределах 1 ≤
этой общей группы классов лежит в пределах 1 ≤  <≤ h*φ (>
<≤ h*φ (> ), где h - порядок абсолютной группы Куммера, φ - функция Эйлера. Для разных модулей
), где h - порядок абсолютной группы Куммера, φ - функция Эйлера. Для разных модулей  1 и
1 и  2 группы классов могут быть эквивалентными, если Н
2 группы классов могут быть эквивалентными, если Н 1 и H
1 и H 2 состоят фактически из одних и тех же прогрессий по (mod f), где / = (
2 состоят фактически из одних и тех же прогрессий по (mod f), где / = ( 1,
1,  2). Если условиться не различать эквивалентные группы классов, то будет получено понятие группы классов в смысле Вебера с ведущим модулем f, к-рый равен наибольшему общему делителю всех эквивалентных модулей. Полем классов в смысле Вебера наз. поле К/k, в к-ром простые идеалы его главного класса Нf и только они, вполне разложимы. Их бесконечность следует из теоремы Дирихле о простых идеалах в прогрессиях, к-рая справедлива для любого поля k. В нек-рых частных случаях Г. Вебер доказал изоморфность группы Галуа поля классов G(K/k) и группы классов Аf /Hf поля k.
2). Если условиться не различать эквивалентные группы классов, то будет получено понятие группы классов в смысле Вебера с ведущим модулем f, к-рый равен наибольшему общему делителю всех эквивалентных модулей. Полем классов в смысле Вебера наз. поле К/k, в к-ром простые идеалы его главного класса Нf и только они, вполне разложимы. Их бесконечность следует из теоремы Дирихле о простых идеалах в прогрессиях, к-рая справедлива для любого поля k. В нек-рых частных случаях Г. Вебер доказал изоморфность группы Галуа поля классов G(K/k) и группы классов Аf /Hf поля k.
К Д. Гильберту (D. Hilbert) восходит совершенно новая точка зрения на теорию полей классов, к-рая сохранилась до настоящего времени. Он понял, что между всеми относительно абелевыми расширениями поля k и всеми полями классов для этого поля должно существовать взаимно однозначное соответствие. Это соответствие выглядит так. Если для нек-рого ведущего модуля f построить группу классов Вебера, то найдется только одно нормальное расширение К/k, в к-ром простые идеалы главного класса Вебера, и только они, будут целиком распадаться, причем группа Галуа поля К/k изоморфна группе классов Вебера, а дискриминант D поля К/k состоит из тех же простых идеалов, что и ведущий модуль f. Верно и обратное: если дано нек-рое абелево расширение К/k с группой Галуа G(K/k), то существует правило (сформулированное впоследствии Т. Такаги), по к-рому можно однозначно построить главный класс Нf так, что группа классов Af /Hf изоморфна группе Галуа G(K/k), и только простые идеалы главного класса Hf вполне разложимы в K, а ведущий модуль f имеет те же простые делители, что и дискриминант D поля К/k. Эта двойственность полей классов и абелевых расширений была высказана Д. Гильбертом в 1900 в качестве гипотезы (доказательства были даны им лишь для частных случаев). В общем виде она доказана Т. Такаги.
Следующий важный этап в развитии теории полей классов связан с именем Э. Артина (Е. Artin), выявившего особую роль канонич. изоморфизма между группой Галуа и группой классов идеалов и показавшего, что эту роль играет Фробениуса автоморфизм σ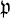 абелевого расширения К/k, к-рый задается сравнением
абелевого расширения К/k, к-рый задается сравнением
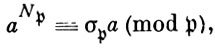
где N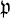 - абсолютная норма идеала
- абсолютная норма идеала 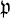 , а пробегает все числа поля K,
, а пробегает все числа поля K, 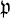 - простой идеал поля к. Автоморфизм σ
- простой идеал поля к. Автоморфизм σ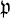 (имеющий теперь обозначение
(имеющий теперь обозначение 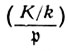 зависит только от класса идеалов, к-рому принадлежит
зависит только от класса идеалов, к-рому принадлежит 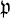 , и обладает мультипликативным свойством.
, и обладает мультипликативным свойством.
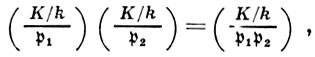
причем символ в правой части понимается как автоморфизм класса, к-рому принадлежит 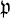 1
1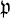 2 . На основании этого Э. Артин ввел символ
2 . На основании этого Э. Артин ввел символ 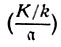 на всей группе Af идеалов а поля k, взаимно простых с ведущим модулем f. Он наз. символом Артина и осуществляет изоморфизм группы классов Af /Hf и группы Галуа G(K/k), явный вид к-рого выражается законом взаимности Артина
на всей группе Af идеалов а поля k, взаимно простых с ведущим модулем f. Он наз. символом Артина и осуществляет изоморфизм группы классов Af /Hf и группы Галуа G(K/k), явный вид к-рого выражается законом взаимности Артина
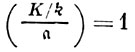
только в том случае, если 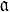 ∈ Hf (взаимность понимается пока в групповом смысле, как соответствие между G(K/k) и Af /Hf). Отсюда можно получить классич. форму взаимности закона на языке символа Куммера степенного вычета (рассмотрев поле
∈ Hf (взаимность понимается пока в групповом смысле, как соответствие между G(K/k) и Af /Hf). Отсюда можно получить классич. форму взаимности закона на языке символа Куммера степенного вычета (рассмотрев поле 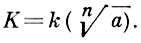 . Из этой формы, в свою очередь, можно получить закон взаимности на языке символа Гильберта. Во всех трех видах закон взаимности рассматривается как изоморфизм групп, а символы Артина, Куммера и Гильберта - как групповые элементы, осуществляющие этот изоморфизм. Но каждый из них имеет и численное значение, равное нек-рому корню n-й степени из 1. Поэтому закон взаимности может быть сформулирован в следующей форме. Если известно значение символа
. Из этой формы, в свою очередь, можно получить закон взаимности на языке символа Гильберта. Во всех трех видах закон взаимности рассматривается как изоморфизм групп, а символы Артина, Куммера и Гильберта - как групповые элементы, осуществляющие этот изоморфизм. Но каждый из них имеет и численное значение, равное нек-рому корню n-й степени из 1. Поэтому закон взаимности может быть сформулирован в следующей форме. Если известно значение символа 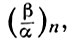 то требуется выяснить, каково значение взаимного к нему символа (β /α)n т. е. выяснить явный вид функции от (α, β), определяющий произведение
то требуется выяснить, каково значение взаимного к нему символа (β /α)n т. е. выяснить явный вид функции от (α, β), определяющий произведение 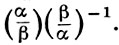 Именно в такой форме этот закон и появился впервые у К. Гаусса (см. Гаусса закон взаимности) для квадратичного поля и у Э. Куммера для кругового поля простой степени. В дальнейшем К. Якоби (С. Jacobi), Ф. Г. М. Эйзенштейн (F. G. М. Eisenstein), Д. Гильберт, X. Хассе (Н. Hasse) и др. продолжали исследование закона взаимности в таком виде, но ими были получены лишь частные результаты. В общем виде эта проблема была решена в 1948 И. Р. Шафаревичем [6] на основе идеи, состоящей в выявлении связи между арифметич. определением символа
Именно в такой форме этот закон и появился впервые у К. Гаусса (см. Гаусса закон взаимности) для квадратичного поля и у Э. Куммера для кругового поля простой степени. В дальнейшем К. Якоби (С. Jacobi), Ф. Г. М. Эйзенштейн (F. G. М. Eisenstein), Д. Гильберт, X. Хассе (Н. Hasse) и др. продолжали исследование закона взаимности в таком виде, но ими были получены лишь частные результаты. В общем виде эта проблема была решена в 1948 И. Р. Шафаревичем [6] на основе идеи, состоящей в выявлении связи между арифметич. определением символа 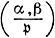 с аналитич. определением абелевого дифференциала α ⋅ dβ на римановой поверхности, И. Р. Шафаревичем была создана конструкция символа
с аналитич. определением абелевого дифференциала α ⋅ dβ на римановой поверхности, И. Р. Шафаревичем была создана конструкция символа 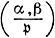 к-рая в точности соответствует определению вычета абелева дифференциала α ⋅ dβ в
к-рая в точности соответствует определению вычета абелева дифференциала α ⋅ dβ в 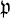 - адическом поле. Для этого он ввел Е-функции, наз. также функциями Шафаревича, на языке к-рых и получил явный вид закона взаимности в общем случае.
- адическом поле. Для этого он ввел Е-функции, наз. также функциями Шафаревича, на языке к-рых и получил явный вид закона взаимности в общем случае.
В конце 20-х гг. 20 в. X. Хассе ввел в теорию полей классов локальный принцип и передоказал многие теоремы для случая абелевого расширения Кp локального поля kp . Первоначально этот принцип играл второстепенную роль (он получался в качестве следствия глобальной теории). Но в конце 30-х гг. К. Шевалле (С. Chevalley) показал необычайную важность локальной точки зрения для всего здания теории полей классов. Он ввел понятие группы иделей и на ее языке изложил общую теорию полей классов с локальной точки зрения. После этого в теории полей классов утвердился локально глобальный принцип. В дальнейшем он развивался и дополнялся (см. [5]), и в результате теория полей классов для абелевых расширений приняла стройный и завершенный вид. Встал вопрос о создании неабелевой теории полей классов для нормальных расширений с неабелевой группой Галуа.
Все вышеизложенное относилось к качественным сторонам А. т. ч. В вопросах количественных оценок и методов их получения А. т. ч. тесно переплетается с аналитич. теорией чисел. Она также базируется в значительной мере на свойствах ζ-функций и L-рядов алгебраич. полей.
Лит. : [1] Боревич 3. И., Шафаревич И. Р., Теория чисел, 2 изд., М., 1972; [2] Постников М. М., Теория Галуа, М., 1963; [3] Вейль Г., Алгебраическая теория чисел, пер. с англ., М., 1947; [4] Ленг С., Алгебраические числа, пер. с англ., М., 1966; [5] Алгебраическая теория чисел, пер. с англ., М., 1969; [6] Шафаревич И. Р., «Матем. сб. », 1950 т 26, в. 1, с. 113-46; [7] Проблемы Гильберта, М., 1969; [8] Artin Е., Tate J., Class field theory, N. Y. - [a. o.], 1967; [9] Weil A., Basic number theory, В., - [а. о.], 1967; [10] Lang S., Algebraic numbers, Reading [Mass.], 1964; [11] Бурбаки H., Коммутативная алгебра, пер. с франц., М., 1971.
А. И. Виноградов.
Источники:
- Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'