АЛГЕБРАИЧЕСКАЯ СИСТЕМА

Расстановка ударений: АЛГЕБРАИ`ЧЕСКАЯ СИСТЕ`МА

АЛГЕБРАИЧЕСКАЯ СИСТЕМА - множество с определенными на нем операциями и отношениями. А. с. принадлежат к числу основных математич. структур и имеют глубоко разработанную общую теорию, сформировавшуюся в начале 50-х гг. 20 в. на грани между алгеброй и математич. логикой.

Основные понятия. Алгебраической системой наз. объект А = 〈 А, О, R〉, состоящий из непустого множества А, семейства О алгебраических операций о_i : А^n_i → А (i ∈ I) и семейства R отношений r_i ⊆ A^m_j (j ∈ J) заданных на множестве А. Показатели n_i, m_j рассматриваемых декартовых степеней множества А предполагаются целыми неотрицательными числами и наз. арностями соответствующих операций и отношений. Множество А наз. носителем, или основным множеством, А. с. А, а его элементы - элементами этой системы. Мощность |А| множества А наз. мощностью, или порядком, А. с. А . Образ о_i (a₁, ..., a_ni) элемента (a₁, ..., a_ni) ∈ A^n_i при отображении о_i : A^n_i → А наз. значением операции о_i в точке (a₁, ..., a_ni). Аналогично, если (a₁, ..., a_mj) ∈ r_j, то говорят, что элементы a₁, ..., a_mj из А находятся в отношении r_j, и пишут r_j (a₁, ..., a_mj). Операции о_i (i ∈ I) и отношения r_j (j ∈ J), в отличие от других операций и отношений, к-рые могут быть определены на множестве А, наз. основными, или главными.

Пара семейств 〈 {n_i : i ∈ I}; {m_j : j ∈ J} 〉 наз. типом

А. с. А . Две А. с. А, А ' однотипны, если I = I', J = J' и n_i = n'_i, m_j = m'_j для всех i ∈ I, j ∈ J. Основные операции о_i, о'_i и основные отношения r_j, r'_j однотипных А. с. А, А ', имеющих одинаковые индексы в I, J соответственно, наз. одноименными. А. с. А наз. конечной, если множество А конечно, и конечного типа, если множество I ∪ J конечно. А. с. А конечного типа записывают в виде А = 〈 А; o₁, ..., o_s, r₁, ..., r_t 〉. А. с. А = 〈 А, О, R〉 наз. универсальной алгеброй, или алгеброй, если множество R основных отношений ее является пустым, и моделью, или реляционной системой, если множество О основных операций ее пустое. Классическими А. с. являются группы, кольца, линейные пространства, линейные алгебры, линейно упорядоченные множества, линейно упорядояенные группы, линейно упорядояенные кольца, решетки и т. д.

Непустое подмножество В основного множества А А. с. А = 〈 А, О, R〉 наз. замкнутым, если для любых элементов b₁, ..., b_ni из В значение о_i (a₁, ..., a_ni) каждой основной операции о_i ∈ O также принадлежит множеству В. Рассматривая операции из О и отношения из R на замкнутом подмножестве В, мы получим А. с. B = 〈 B, О, R〉, однотипную данной и наз. подсистемой А. с. A . Подсистемы алгебр наз. подалгебрами, а подсистемы моделей - подмоделями. Понятие подалгебры существенно зависит от множества основных операций рассматриваемой алгебры. Напр., группоид G есть алгебра типа 〈 2 〉, т. е. алгебра с одной основной операцией G × G → G. Группоид H с выделенной единицей е есть алгебра типа 〈 2, 0 〉, выделенный элемент к-рой обладает по отношению к основной операции о: H × H → H свойством о(е, h) = o(h, e) = h для всех h ∈ H. Поэтому всякий подгруппоид группоида H с выделенной единицей е содержит е, тогда как подгруппоид группоида 〈 Н, о〉 не обязан содержать элемент е. В отличие от алгебр, любое непустое подмножество модели может рассматриваться как подмодель.

А. с. A изоморфна однотипной А. с. A ', если существует такое взаимно однозначное отображение φ множества А на множество А', что

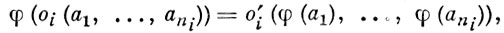
(1) 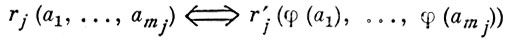(2)

для всех а₁, а₂,... из А и для всех i ∈ I, j ∈ J. Отображение φ с этими свойствами наз. изоморфизмом.

Под классом алгебраич. систем понимается в дальнейшем только абстрактный класс, т. е. такой класс однотипных А. е., к-рый содержит с каждой системой А и все изоморфные ей системы. При рассмотрении того или иного класса А. с. все системы из этого класса записывают обычно в определенной сигнатуре следующим образом. Пусть класс имеет тип 〈 {ni : i ∈ I}, {mj : j ∈ J}〉. Каждому i ∈ I сопоставляют нек-рый символ Fi, наз. функциональным, а каждому j ∈ J - символ Рj, наз. предикатным. Если А. с. А принадлежит классу и оi : Ani → А - основная операция в ней, то элемент оi (a1, ..., ani) из А записывают в виде Fi (a1, ..., ani). Аналогично, если rj ⊆ Amj - основное отношение в А и элемент (a1, ..., amj) ∈ rj, то пишут Pj (a1, ..., amj) = И (истинно) или просто Рj (a1, ..., amj). Если же (a1, ..., amj) ∉ rj, то пишут Pj (a1, ..., amj) = Л (ложно) или ⅂Р(a1, ..., amj). Пусть Ωf = {Fi : i ∈ I}, Ωp = {Pj : j ∈ J} и ν - отображение объединения Ωf ∪ Ωp в множество натуральных чисел {0, 1, 2,...}, определяемое формулами: ν (Fi) = ni (i ∈ I), ν (Pj) = mj (j ∈ J). Объект Ω = 〈 Ωf, Ωp, ν 〉 наз. сигнатурой класса . Конечную сигнатуру записывают в виде строки 〈 Fn11, ..., Fnss ; Pm11, ..., Pmtt 〉 или короче 〈 F1, ..., Fs ; P1, ..., Pt 〉. А. с. А, записанная в сигнатуре Ω, наз. Ω-cистемой и обозначается А = 〈 A, Ω 〉.

Условия (1), (2) изоморфизма однотипных систем А, А ' упрощаются, если эти системы рассматривать в одной сигнатуре Ω. Так, если сигнатурными символами будут F_i (i ∈ I), P_j (j ∈ J), то (1), (2) примут вид

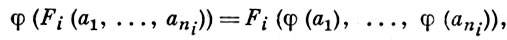
(3) 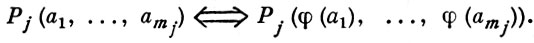(4)

Гомоморфизмом Ω-системы А в Ω-систему А ' наз. всякое отображение φ : А → А', удовлетворяющее условию (3) и условию

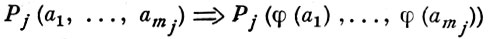
(5)

для всех F_i ∈ Ω_f, P_j ∈ Ω_p и для всех а₁, а₂,... из А . Гомоморфизм φ : А → А ' наз. сильным, если для любых элементов b₁, ..., b_mj из А' и для любого предикатного символа P_j из Ω_p соотношение P_j (b₁, ..., b_mj) = И влечет существование в А таких прообразов a₁, ..., a_mj элементов b₁, ..., b_mj, для к-рых P_j (b₁, ..., b_mj) = И. Понятия гомоморфизма и сильного гомоморфизма алгебр совпадают. Для моделей существуют гомоморфизмы, к-рые не являются сильными, и взаимно однозначные гомоморфизмы, к-рые не являются изоморфизмами. При гомоморфизме φ : А → А ' образами в А ' подсистем из А и непустыми полными прообразами в А подсистем из А ' являются подсистемы.

Эквивалентность θ ⊆ А × А наз. конгруэнцией Ω-системы А, если

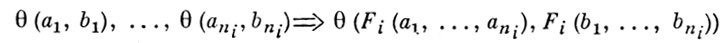
для всех a₁, b₁, ..., a_ni, b_ni из А и для всех F_i ∈ Ω_f . Для каждого гомоморфизма φ А. с. А бинарное отношение θ (а, b), истинное тогда и только тогда, когда φ (а) = φ (b), является конгруэнцией в А, к-рая наз. ядерной. Для произвольной конгруэнции θ Ω-системы А и для каждого элемента a ∈ А множество a/θ = {х ∈ А : θ (x, а)}, наз. смежным классом А. с. А по конгруэнции θ. Полагая для каждых F_i ∈ Ω_f, P_j ∈ Ω_p,

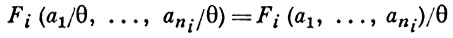
и

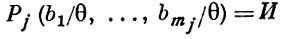
тогда и только тогда, когда существуют такие элементы c₁, ..., c_mj в А, что θ (b₁, c₁), ..., θ (b_mj, c_mj) и P_j (c₁, ..., c_mj), мы получим А. с. А /θ, однотипную данной и наз. факторсистемой А. с. А по конгруэнции θ. Для каждой конгруэнции θ А. с. А канонич. отображение φ (а) = а/θ (а ∈ А) является гомоморфизмом А. с. А на факторсистему А /θ, для которого данная конгруэнция θ ядерная. Если φ есть гомоморфизм А. с. А на А. с. А ' и θ-ядерная конгруэнция для φ, то отображение ψ (а/θ) = φ (а) является гомоморфизмом факторсистемы А /θ на А. с. А '. Если при этом гомоморфизм φ сильный, то ψ есть изоморфизм.

Декартовым произведением Ω-систем А_α = 〈 А_α, Ω 〉 (α ∈ Λ ≠ ∅) наз. Ω-система D = 〈 D, Ω 〉, в к-рой D есть декартово произведение основных множеств А_α (α ∈ Λ), а основные операции и основные отношения на D задаются условиями: F_i (d₁, ..., d_ni) (d₁, ..., d_ni ∈ D, F_i ∈ Ω_f) есть элемент d ∈ D с координатами d(α) = F_i (d₁ (α), ..., d_ni (α)) (α ∈ Λ), P_j (d₁, ..., d_mj) = И (P_j ∈ Ω_p) тогда и только тогда, когда P_j (d₁ (α), ..., d_mj (α)) = И для всех α ∈ Λ.

Язык 1-й ступени. Основным формальным языком теории А. с. является язык 1-й ступени L, к-рый строится следующим образом. Алфавит языка L в заданной сигнатуре Ω = 〈 Ω_f, Ω_p, ν 〉, Ω_f = {F_i ; i ∈ I}, Ω_p = {P_j ; j ∈ J}, состоит из предметных переменных х₁, х₂, ..., функциональных символов F_i (i ∈ I), предикатных символов P_j (j ∈ J), символов логич. связок:

кванторов:

∀ x_k - «для каждого элемента х_k »,

∃ x_k - «существует такой элемент х_k »

и вспомогательных символов: скобок и запятых. Для выражения свойств (1-й ступени) Ω-систем употребляются конечные последовательности алфавитных символов, или слова, составленные по определенным правилам и наз. термами и формулами. Индуктивно полагают, что каждое слово вида x_k или F_i при ν (F_i) = 0 есть терм; если f₁, ..., f_n - термы и n = ν (F_i), то F_i (f₁, ..., f_n) - также терм.

Если А есть Ω-система и f(х₁, ..., х_n) - терм сигнатуры Ω, содержащий предметные переменные х₁, ..., х_k, то, заменяя х₁, ..., х_k к.-н. элементами a₁, ..., a_k из А и выполняя над последними операции в А, соответствующие входящим в терм символам из Ω_f, получают элемент f(a₁, ..., a_k) из А, называемый значением терма f(x₁, ..., x_k) при x₁ = a₁, ..., x_k = a_k . Если φ - гомоморфизм Ω-системы А в Ω-систему А ', то

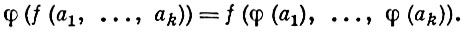
Понятие формулы сигнатуры Ω, свободных и связанных предметных переменных в ней определяется также индуктивно:

1) Если Р - какой-нибудь предикатный символ из Ω или знак равенства =, m = ν (Р) или 2 соответственно, а f₁, ..., f_m - произвольные термы сигнатуры Ω, то слово P(f₁, ..., f_m) есть формула, в к-рой все предметные переменные свободны.

2) Если - формула, то ⅂ - также формула. Свободные (связанные) предметпые переменные в формуле ⅂ те и только те, к-рые являются свободными (связанными) в .

3) Если ₁, ₂ - формулы и предметные переменные, входящие одновременно в обе эти формулы, свободны в каждой из них, то слова

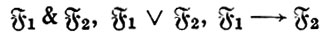
(6)

- также формулы.

Предметные переменные, свободные (связанные) хотя бы в одной из формул ₁, ₂, наз. свободными (связанными) и в формулах (6).

4) Если предметное переменное x_k входит свободно в формулу то слова (∀ x_k) , (∃ х_k) снова являются формулами, в к-рых переменное x_k связанное, а все остальные предметные переменные, входящие в формулу свободно или связанно, остаются такими же и в формулах (∀ x_k) , (∃ х_k) .

Если заданы Ω - система А и формула сигнатуры Ω, то придавая всем свободным предметным переменным х₁, ..., х_k в какие-нибудь значения a₁, ..., a_k из А и интерпретируя функциональные и предикатные символы, входящие в , как соответствующие основные операции и основные отношения в А, мы получим конкретное высказывание, к-рое будет истинным или ложным. В соответствии с этим формуле приписывают значение И или Л при х₁ = a₁, ..., х_k = a_k, обозначаемое (a₁, ..., a_k). Если φ - изоморфное отображение Ω-системы А на Ω-систему А ', то

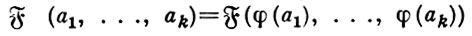
для всех a₁, ..., a_k из А.

Формула наз. замкнутой, если она не содержит свободных предметных переменных. Для любой замкнутой формулы сигнатуры Ω и произвольной Ω-системы А можно говорить об истинности или ложности в А . Совокупность S замкнутых формул данной сигнатуры Ω наз. выполнимой, или совместной, если существует Ω-система, в к-рой истинны все формулы из S.

Теорема компактности или локальная теорема Гёделя-Мальцева. Если выполнима каждая конечная часть бесконечной совокупности S замкнутых формул какой-то сигнатуры Ω, то выполнима и вся совокупность S.

Аксиоматизируемые классы. Пусть S - некоторая совокупность замкнутых формул сигнатуры Ω. Класс всех Ω-систем, в к-рых истинны все формулы из S, будет обозначаться КS. Совокупность Th всех замкнутых формул сигнатуры Ω, истинных во всех Ω-системах из заданного класса , наз. элементарной теорией класса . В частности, если (А ) - класс Ω-систем, изоморфных данной Ω-системе А, то Th(А ) наз. элементарной теорией Ω-системы А и обозначается просто Th А . Класс Ω-систем наз. аксиоматизируемым, если = KTh . Класс Ω-систем аксиоматизируем тогда и только тогда, когда существует такая совокупность S замкнутых формул сигнатуры Ω, что = KS.

Наряду с общим понятием аксиоматизируемости рассматривают аксиоматизируемость при помощи формул 1-й ступени специального вида. Наиболее важными в алгебре специальными формулами заданной сигнатуры Ω являются:

Тождества - формулы вида

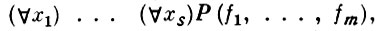
где Р - к.-л. предикатный символ из Ω или знак равенства =, а f₁, ..., f_m - термы сигнатуры Ω от х₁, ..., х_s .

Квазитождества - формулы вида

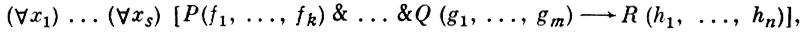
где P, ..., Q, R - нек-рые предикатные символы из Ω_p или знаки равенства, a f₁, ..., f_k, g₁, ..., g_m, h₁, ..., h_n - термы сигнатуры Ω от х₁, ..., х_s .

Универсальные формулы - формулы вида (∀ х₁), ..., (∀ х_s) где - формула сигнатуры Ω, не содержащая кванторов.

Если задано множество S тождеств (квазитождеств или универсальных формул) сигнатуры Ω, то класс KS наз. многообразием (квазимногообразием или универсальным классом) Ω-систем.

Теорема Биркгофа. Непустой класс Ω-систем является многообразием тогда и только тогда, когда он замкнут относительно подсистем, декартовых произведений и гомоморфных образов.

Если А = 〈 A, Ω 〉 - некоторая Ω-система, то, заменяя каждый функциональный символ F_i из Ω_f предикатным символом F*_i арности n_i + 1 (на 1 выше) и полагая для элементов a₁, ..., a_ni, а из А

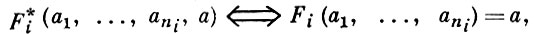
мы получим модель А * = 〈 A, Ω * 〉, для которой Ω *_p = Ω_p ∪ {F*_i : F_i ∈ Ω_f}. Подмодели модели А * наз. подмоделями Ω-системы А . Для любых непустых конечных подмножеств А_α ⊆ А, Ω *_β ⊆ Ω * модель А_{α β} = 〈 А_α, Ω *_β 〉 наз. конечным обеднением конечной подмодели А_α = 〈 А_α, Ω *〉 Ω-системы А . Ω-система А наз. локально вложимой в класс Ω-систем, если для каждого конечного обеднения А_{α β} любой конечной подмодели А_α Ω-системы А существует в классе такая Ω-система B (зависящая от выбранного конечного обеднения А_{α β}), что модель А_{α β} = 〈 А_α, Ω *_β 〉 изоморфна модели B_{α β} = 〈 B_α, Ω *_β 〉 для подходящего подмножества B_α ⊆ B.

Подкласс 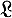класса Ω-систем наз. универсальным (или универсально аксиоматизируемым) в , если существует такая совокупность S универсальных формул сигнатуры Ω, что 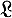= KS ∩ .

Теорема Тарского-Лося. Подкласс 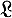класса Ω-систем универсален в тогда и только тогда, когда 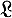содержит все системы из , локально вложимые в .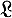

Фильтрованные произведения. Пусть D = ∏ А_α - декартово произведение Ω-систем А_α (α ∈ Λ, Λ ≠ ∅) и Ф - некоторый фильтр над Λ. Отношение

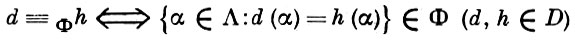
есть эквивалентность на основном множестве D Ω-системы D . Для каждого элемента d ∈ D пусть d/Ф есть смежный класс по этой эквивалентности и D/Ф = {d/Ф : d ∈ D}. Полагая

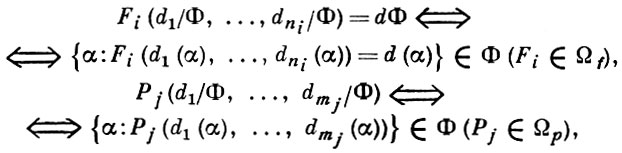
можно получить Ω-систему D /Ф = (D/Ф, Ω), которая наз. фильтрованным по фильтру Ф произведением Ω-систем А_α (α ∈ Λ). Ω-системы А_α (α ∈ Λ) наз. сомножителями этого произведения. Если Ф - ультрафильтр над Λ, то фильтрованное произведение D /Ф наз. ультрапроизведением Ω-систем А_α (α ∈ Λ).

Теорема об ультрапроизведениях. Если D /Ф - ультрапроизведение Ω-систем А_α (α ∈ Λ) и (х₁, ..., х_k) - произвольная формула сигнатуры Ω, в к-рой свободными предметными переменными являются х₁, ..., х_k, то для любых элементов d₁, ..., d_k ∈ D

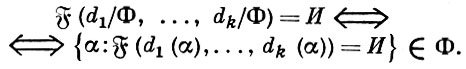
В частности, замкнутая формула сигнатуры Ω истинна в ультрапроизведении D /Ф Ω-систем А_α (α ∈ Λ) тогда и только тогда, когда множество номеров сомножителей, в к-рых формула истинна, принадлежит ультрафильтру Ф. Поэтому всякий аксиоматизируемый класс Ω-систем замкнут относительно ультрапроизведений.

Класс L Ω-систем универсально аксиоматизируем тогда и только тогда, когда он замкнут относительно подсистем и ультрапроизведений.

Ω-система E = 〈 {е}, Ω 〉 наз. единичной, если ее основное множество состоит из одного элемента, скажем е, и P_j (e, ..., е) = И для всех Р_j ∈ 8712; Ω_p .

Теорема Мальцева. Класс Ω-систем является квазимногообразием тогда и только тогда, когда он содержит единичную Ω-систему и замкнут относительно подсистем и фильтрованных (по произвольному фильтру) произведений.

Полнота и категоричность. Непустой класс Ω-систем наз. категоричным, если все Ω-системы из изоморфны между собой. Всякий категоричный аксиоматизируемый класс Ω-систем состоит из одной (с точностью до изоморфизма) конечной Ω-системы.

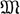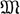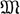Класс Ω-систем наз. категоричным в мощности , если он содержит Ω-систему мощности и все Ω-системы из , имеющие мощность , изоморфны между собой. Напр., класс алгебраически замкнутых полей фиксированной характеристики категоричен в любой несчетной бесконечной мощности. Непустой класс Ω-систем наз. полным, если для любых Ω-систем А, B из имеет место равенство ТhА = Th B .

Теорема Booта. Если аксиоматизируемый класс Ω-систем категоричен в нек-рой мощности 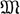≥ |Ω_f ∪ Ω_p | и все Ω-системы из бесконечны, то - полный класс.

В частности, класс всех алгебраически замкнутых полей фиксированной характеристики является полным.

См. также Алгебраической системы автоморфизм, Алгебраических систем квазимногообразие, Алгебраических систем класс, Алгебраических систем многообразие.

Лит. : [1] Мальцев А. И., Алгебраические системы, М., 1970; [2] Кон П., Универсальная алгебра, пер. с англ., М., 1968; [3] Grätzеr G., Uneversal algebra, Princeton, 1968; [4] Веll J. L., Slomson А. В., Models and ultraproducts, Amst. - L., 1969; [5] Chang С. С, Кeisler H. J., Model theory, Amst. - N. Y., 1973.

Д. M. Смирнов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.