АЛГЕБРА ФУНКЦИЙ

Расстановка ударений: А`ЛГЕБРА ФУ`НКЦИЙ

АЛГЕБРА ФУНКЦИЙ - полупростая коммутативная банахова алгебра А, реализованная в виде алгебры непрерывных функций на пространстве максимальных идеалов. Если а ∈ А и f - нек-рая функция, определенная на спектре элемента a (т. е. на множестве значений функции â = а), то f(a) есть нек-рая функция на . Условие f(a) ∈ A, конечно, не обязано выполняться. Если, однако, f - целая функция, то f(a) ∈ A для любого а ∈ А. Использование интегральной формулы Коши позволяет существенно усилить этот результат: если функция f регулярна в нек-рой окрестности спектра элемента а, то f(a) ∈ A, и отображение f → f(а) является гомоморфизмом А. ф., аналитических в нек-рой окрестности спектра элемента а ∈ А, в алгебру А. Это утверждение остается справедливым и для неполупростых коммутативных банаховых алгебр. Кроме того, класс функций, аналитических в окрестности спектра данного элемента, может оказаться не расширяемым: напр., если A = L¹ (ℤ) и f(a) ∈ A для всех а ∈ А, спектр к-рых принадлежит отрезку [0, 1], то f аналитична в нек-рой окрестности этого отрезка.

В отдельных случаях элемент f(a) можно определить и для многозначных аналитич. функций f, но это определение встречает естественные затруднения. Напр., пусть А - алгебра непрерывных функций в круге |z| ≤ 1 аналитических в круге |z| < 1 и удовлетворяющих условию f'(0) = 0. Единичный круг естественно отождествляется с пространством максимальных идеалов А. Непрерывная на пространстве максимальных идеалов функция f₁ (z) = z не принадлежит алгебре А, но является решением квадратного уравнения

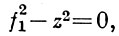
где z² ∈ A.

Если А - полупростая алгебра с пространством максимальных идеалов А, f ∈ С(X),

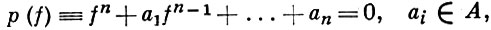
р'(f) ∈ ε (A) (простой корень), то f ∈ A. Аналогично, если f ∈ С(X) и exp f ∈ A, то f ∈ A.

А. ф. наз. алгеброй с равномерной сходимостью, если норма в этой алгебре определяет сходимость, эквивалентную равномерной сходимости функций â на пространстве максимальных идеалов. Если ||а² || = ||а||² для всех а ∈ А, то А - алгебра с равномерной сходимостью. Общим примером алгебры с равномерной сходимостью является замкнутая подалгебра в алгебре ограниченных непрерывных функций на некотором топологич. пространстве, наделенной естественной sup-нормой.

Если А - алгебра с равномерной сходимостью, и ее пространство максимальных идеалов метризуемо, то среди всех кольцевых границ (не только замкнутых) существует минимальная граница Г₀, замыканием к-рой служит граница Шилова. Множество Г₀ состоит из «точек пика»: х₀ наз. точкой пика, если существует такая функция f ∈ A, что |f(х)| < |f(х₀)| для всех х ≠ х₀ . В рассматриваемом случае для любой точки из пространства максимальных идеалов существует представляющая мера, сосредоточенная на Г₀ .

А. ф. наз. аналитической, если всякая функция из этой алгебры, равная нулю на непустом открытом подмножестве пространства максимальных идеалов, равна нулю тождественно. Аналогично определяются алгебры, аналитические относительно границы. Всякая аналитич. алгебра является аналитической относительно границы Шилова; обратное, вообще говоря, неверно.

А. ф. А наз. регулярной, если для любого замкнутого множества F в пространстве А максимальных идеалов алгебры А и любой не содержащейся в F точки х₀ найдется такая функция f ∈ A, что f(x) = 1 для всех x ∈ F и f(х₀) = 0. Всякая регулярная алгебра нормальна, т. е. для любой пары непересекающихся замкнутых множеств F, F₀ ⊂ X существует элемент f ∈ A такой, что f(x) = 1 для всех x ∈ F и f(x₀) = 0 для всех x ∈ F₀ . Более того, в регулярной алгебре для любого конечного открытого покрытия {U_i}, 1 ≤ i ≤ m, пространства X имеется разбиение единицы, принадлежащее А, т. е. система функций f₁, ..., f_n ∈ A, для к-рых

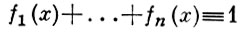
и

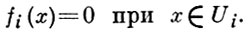
Функция g наз. локально принадлежащей А. ф. А, если для любой точки х₀ ∈ Х существует такая окрестность, в к-рой эта функция совпадает с нек-рой функцией из алгебры. Всякая функция, локально принадлежащая регулярной алгебре, сама является элементом этой алгебры.

Элемент f А. ф. наз. вещественным, если f^(x) вещественно при всех х ∈ Х. Если А - алгебра с вещественными образующими f_α и

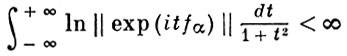
для всех f_α, то А регулярна.

Идеал в банаховой алгебре наз. примарным, если он содержится только в одном максимальном идеале. Если А - регулярная А. ф., то в каждом максимальном идеале х₀ имеется наименьший замкнутый примарный идеал J(x₀), к-рый содержится в любом замкнутом примарном идеале, содержащемся в х₀ ; идеал J(х₀) есть замыкание идеала, образованного функциями f ∈ A, равными нулю в нек-рой (зависящей от f) окрестности точки х₀ ∈ Х.

В алгебре абсолютно сходящихся интегралов Фурье c присоединенной единицей всякий максимальный идеал совпадает с соответствующим примарным идеалом.

Пусть А - замкнутая подалгебра алгебры С(X), где А - нек-рый компакт (не обязательно совпадающий с пространством максимальных идеалов алгебры А). Пусть А разделяет точки компакта А, т. е. для любых двух различных точек х₁, х₂ ∈ Х существует такая функция f из алгебры А, для к-рой f(x₁) ≠ f(x₂). Алгебра A наз. симметричной, если вместе с функцией f алгебре принадлежит и функция 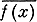. Согласно теореме Стоуна-Вейерштрасса, если А симметрична, то А = С(Х). Алгебра A наз. антисимметричной, если из условий f ∈ A, 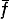∈ A следует, что f - постоянная функция. Антисимметричными являются, в частности, алгебры аналитич. функций. Подмножество S ⊂ X наз. множеством антисимметрии (относительно алгебры А), если любая функция f ∈ A, вещественная на S, постоянна на этом множестве. Согласно этому определению алгебра А антисимметрична, если все X являются множеством антисимметрии. В общем случае пространство X можно представить в виде объединения непересекающихся замкнутых максимальных множеств антисимметрии. Каждое максимальное множество антисимметрии является пересечением множеств пика (множество Р наз. множеством пика, если существует такая функция f ∈ A, что f|_P = 1 и |f(x)| < 1 при х ∉ Р). Отсюда следует, что сужение А|_Y алгебры А на максимальное множество антисимметрии есть замкнутая (антисимметричная) подалгебра алгебры C(Y). Если X есть пространство максимальных идеалов алгебры А, то максимальные множества антисимметрии связны. Если непрерывная функция такова, что на каждом максимальном множестве антисимметрии она совпадает с нек-рой функцией из алгебры А, то и сама эта функция принадлежит А. Это обобщение теоремы Стоуна-Вейерштрасса позволяет в принципе свести изучение произвольных алгебр с равномерной сходимостью к изучению антисимметричных алгебр А. Вместе с тем изучение произвольных алгебр А не может быть сведено к аналитическим алгебрам: существует пример алгебры типа R(X) (замкнутой подалгебры алгебры С(X)), не совпадающей с С(X), антисимметричной и регулярной.

Пусть Re A - вещественное пространство функций вида Ref, где f ∈ A; если ReA - алгебра, или если ReA замкнуто в С(X), то А = С(Х). Пространство X можно рассматривать как часть пространства максимальных идеалов алгебры А; поэтому на X можно рассматривать не только обычную топологию пространства максимальных идеалов, но и метрику, индуцированную вложением X в пространство, сопряженное А. Расстояние в смысле этой метрики обозначим ρ_A . Для любых точек x₁, х₂ ∈ X имеет место неравенство ρ_A (x₁, х₂) ≤ 2; отношение ρ_A (x₁, х₂) < 2 является отношением эквивалентности, и классы эквивалентности наз. долями Глисона. Если X - круг |z| ≤ 1 и А - замкнутая подалгебра в С(X), состоящая из аналитических при |z| < 1 функций, то метрика ρ_A неевклидова, а долями Глисона служат одноточечные множества на границе и внутренность круга. Доли Глисона не всегда обладают аналитич. структурой: любое σ-компактное вполне регулярное пространство гомеоморфно доле Глисона пространства максимальных идеалов нек-рой алгебры, такой, что сужение алгебры на эту долю содержит всякую ограниченную непрерывную функцию. Принадлежность двух точек к одной и той же доле Глисона может быть охарактеризована в терминах представляющих мер на границе Шилова: такие две точки обладают взаимно абсолютно непрерывными представляющими мерами с ограниченными производными. Алгебра, для к-рой ReA|_Г плотно в С(Г), наз. алгеброй Дирихле; если Р - доля Глисона в пространстве максимальных идеалов алгебры Дирихле, состоящая более, чем из одной точки, то существует такое непрерывное взаимно однозначное отображение ψ круга |z| < на Р, что для любой функции f ∈ А функция f(ψ (z)) аналитична при |z| < 1. Таким образом, Р обладает структурой, относительно к-рой функции f ∈ A аналитичны; отображение ψ, вообще говоря, не является гомеоморфизмом, если Р снабжено обычной топологией пространства максимальных идеалов, но ψ является гомеоморфизмом, если снабдить Р метрикой ρ_A .

Лит. см. при статье Банахова алгебра.

Е. А. Горин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.