АЛГЕБРА С АССОЦИАТИВНЫМИ СТЕПЕНЯМИ

Расстановка ударений: А`ЛГЕБРА С АССОЦИАТИ`ВНЫМИ СТЕПЕНЯ`МИ

АЛГЕБРА С АССОЦИАТИВНЫМИ СТЕПЕНЯМИ - линейная алгебра А над полем F, всякий элемент к-рой порождает ассоциативную подалгебру. Множество всех А. с а. с. над данным полем F образует многообразие алгебр, к-рое в случае, когда характеристика поля F равна 0, задается системой тождеств

(х, х, х) = (х², х, х) = 0,

где (х, у, z) = (xy)z - x(yz). Если F - бесконечное ноле простой характеристики р, то многообразие А. с а. с. не может быть задано никакой конечной системой тождеств, но известна бесконечная независимая система тождеств, определяющая его (см. [3]). Если коммутативная А. с а. с. A характеристики, отличной от 2, обладает идемпотентом е ≠ 0, то для А имеет место пирсовское разложение в прямую сумму векторных подпространств:

(*)

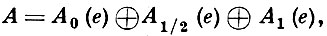
где А_λ (е) = {а ∈ А|ea = λ a), А = 0, ½, 1. При этом А₀ (е) и А₁ (е) - подалгебры, A₀ (e)A₁ (e) = 0, A_½ (e)A_½ (e) ⊆ А₀ (е) + А₁ (е), A_λ (e)A_½ (e) ⊆ A_½ (e) + A_{1 - λ} (e) для λ = 0; 1. Разложение (*) играет фундаментальную роль в структурной теории А. с а. с.

Лит. : [1] Albert A. A., «Trans. Amer. Math. Soc. », 1948, v. 64, № 3, p. 552-93; [2] Гайнов А. Т., «Успехи матем. наук», 1957, т. 12, № 3 (75), с. 141-46; [3] его же «Алгебра и логика», 1970, т. 9, № 1, с. 9-33.

А. Т. Гайнов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.