PI-АЛГЕБРА

Расстановка ударений: PI-А`ЛГЕБРА

PI-АЛГЕБРА - алгебра над полем, в к-рой выполняются нек-рые полиномиальные тождества.

Пусть А - ассоциативная алгебра над полем F,

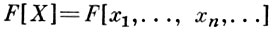
- свободная ассоциативная алгебра (алгебра некоммутативных многочленов) от счетного множества образующих х = (х₁, ..., х_n ...) над F и f(х₁, ..., х_n) - ненулевой элемент алгебры F[x]. Тогда

f(х₁, ..., х_n) = 0

наз. полиномиальным тождеством алгебры А, если f(a₁, ..., a_n) = 0 для любого набора элементов a₁, ..., a_n ∈ А.

Примеры PI-A. и тождеств. В коммутативной алгебре выполняется тождество

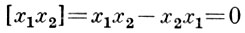
(тождество коммутативности); во внешней алгебре линейного пространства выполняется тождество метабелевости [{х₁, х₂ ], х₃ ] = 0; алгебра А конечной размерности n - 1 над полем F удовлетворяет так наз. стандартному тождеству n-й степени

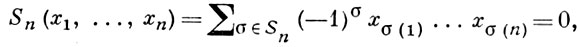
где S_n - группа подстановок множества, состоящего из первых n натуральных чисел и (- 1)^σ = sgnσ, а также более общему тождеству Капелли

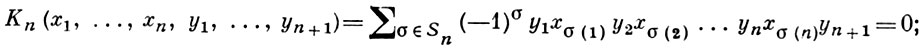
в алгебре F_n квадратных матриц порядка n над полем F выполняется стандартное тождество степени 2n. Тензорное произведение PI-A. является PI-A.

Для всякой PI-A. А над полем F характеристики нуль можно указать такое натуральное число n, что тождества алгебры А исчерпываются степенями тождеств алгебры матриц F_n, причем нек-рая степень любого тождества алгебры F_n является тождеством алгебры А. Таким образом, во всякой PI-A. над полем характеристики нуль выполняется нек-рая степень стандартного тождества.

Совокупность всех левых частей тождеств, выполняющихся в данной алгебре А, образует вполне характеристич. идеал (коротко, Т-идеал) свободной алгебры F[x] и обратно, для всякого Т-идеала существует алгебра, совокупность тождеств к-рой совпадает с этим Т-идеалом (ею будет, напр., факторалгебра F[x]/T). В случае, когда поле F нулевой характеристики, тождества можно дифференцировать, и Т-идеалы алгебры F[x] - это в точности дифференциально замкнутые односторонние идеалы. Напр., из нильтождества хⁿ = 0 многократным дифференцированием получается тождество

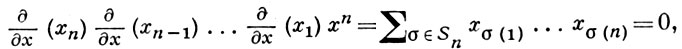
к-рое является полилинейным (точнее, n-линейным), т. е. линейным по каждой переменной, входящей в его запись. Причем и обратно, положив в последнем тождестве х₁ =... = х_n = 0, можно получить тождество n! хⁿ = 0, или хⁿ = 0. Этот процесс линеаризации тождеств позволяет утверждать (в случае полей нулевой характеристики), что все тождества алгебры являются следствиями ее полилинейных тождеств. Для алгебры с единицей, более того, все тождества вытекают из ее полилинейных тождеств, представимых в виде линейных комбинаций произведений правонормированных коммутаторов различных степеней от образующих х_i . Вопрос о том, всякая ли ассоциативная алгебра обладает конечным базисом тождеств, составляет содержание проблемы Шпехта.

Совокупность всех алгебр, удовлетворяющих данной системе тождеств, наз. многообразием. Многообразие может быть определено также как класс алгебр, замкнутый относительно взятия подалгебр, гомоморфных образов и подпрямых произведений (см. также Алгебраических систем многообразие). Для ряда многообразий алгебр доказана их конечная базируемость (т. е. в этих многообразиях положительно решена проблема Шпехта). Таковы многообразия (все над полем нулевой характеристики) нильпотентных алгебр данного индекса п, алгебр, в к-рых аддитивные коммутаторы длины n равны нулю (Ли-нильпотентные алгебры), многообразие алгебр, определяемое Т-идеалом политождеств М₂ - алгебры матриц 2-го порядка. Однако для многообразия, определяемого идеалом тождеств М_n - алгебры матриц порядка n < 2, вопрос открыт.

Наличие полиномиального тождества жестко определяет структуру ассоциативной алгебры. Примитивная алгебра А, удовлетворяющая полиномиальному тождеству степени d, изоморфна алгебре матриц D_n над телом D с центром Z и

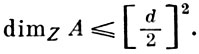
Поэтому полупростая (в смысле Джекобсона радикала) PI-A. разлагается в подпрямую сумму полных матричных алгебр над телами, причем порядки этих алгебр и размерности тел над центрами ограничены в совокупности, и Т-идеал тождеств полупростой алгебры совпадает с нек-рым «матричным» Т-идеалом М_n . Упорядоченная PI-A. коммутативна. Первичная PI-A. А обладает двусторонним классич. кольцом частных Q(A), к-рое изоморфно матричной алгебре D_m над телом D, конечномерным над своим центром Z. Кольцо Q(А) является центральным расширением алгебры А в том смысле, что Q(A) = AZ. Идеалы тождеств алгебр А и Q(А) совпадают. PI-A. удовлетворяют ряду условий «бернсайдовского типа» (см. Бернсайда проблема). Например, алгебраическая (ниль -) PI-A. локально конечна (локально нильпотентна). Ассоциативная нильалгебра ограниченного индекса n нильпотентна, если характеристика основного поля нулевая или больше n.

PI-A., не имеющая ненулевых нильидеалов, представима матрицами над коммутативным кольцом. Но не всякая PI-A. представима в таком смысле. Напр., внешняя алгебра счетномерного пространства не представима - в ней не выполняется никакое стандартное тождество. Внутренняя характеризация представимости алгебры матрицами над коммутативным кольцом составляет самостоятельное направление исследований в теории PI-A.

Радикал Джекобсона конечно порожденной PI-A. над полем нулевой характеристики является нильидеалом. Вопрос о его нильпотентности пока (1977) открыт. Если радикал Джекобсона PI-A. нильпотентен, то она удовлетворяет всем тождествам алгебры матриц порядка n для нек-рого n. Для конечно порожденных алгебр доказано и обратное утверждение. Более того, для конечно порожденной алгебры над полем нулевой характеристики нильпотентность радикала Джекобсона эквивалентна выполнимости в ней нек-рого стандартною тождества.

Во многих случаях выполнимость тождества для «части» элементов алгебры влечет за собой выполнимость нек-рого тождества во всей алгебре. Напр., если в алгебре с инволюцией симметрические элементы удовлетворяют тождеству, то она - PI-A. ; если на алгебре над полем нулевой характеристики действует конечная группа автоморфизмов и подалгебра инвариантов удовлетворяет нек-рому тождеству, то исходная алгебра будет PI-A.

Представляет интерес при каких условиях те или иные алгебры специального типа удовлетворяют полиномиальному тождеству.

Для того чтобы групповая алгебра F(G) группы G над полем нулевой характеристики удовлетворяла некоторому полиномиальному тождеству, необходимо и достаточно, чтобы группа G обладала абелевой подгруппой конечного индекса. Если же характеристика F конечна и равна р, то F[G] является PI-A. тогда и только тогда, когда G обладает р-абелевой подгруппой конечного индекса (группа наз. р-абелевой, если ее коммутант - конечная р-группа).

Универсальная обертывающая алгебра U_L алгебры Ли L над полем F характеристики нуль есть PI-A. в том и только том случае, когда L абелева (U_L коммутативна). Если же F - поле конечной характеристики, то U_L является PI-A. тогда и только тогда, когда L обладает абелевым идеалом конечной коразмерности и присоединенное представление алгебры L является алгебраическим ограниченной степени.

Все PI-подалгебры свободной ассоциативной алгебры коммутативны.

Теория PI-A. является естественным обобщением коммутативной алгебры, она содержит глубокие и законченные аналоги теорем коммутативной алгебры, что позволяет говорить о зарождении некоммутативной алгебраич. геометрии.

Во всякой конечно порожденной PI-A. А с образующими a₁, ..., a_k над полем F выполняется условие ограниченности высот, т. е. существуют конечное число слов v₁, ..., v_m от а_i и натуральное число h такие, что всякое слово u от образующих а_i представимо в А в виде линейной комбинации слов

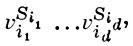
где d ≤ h, совпадающих по составу относительно а_i со словом u. В коммутативном случае в качестве слов v_i можно взять сами образующие а_i . Свободным некоммутативным аффинным кольцом наз. факторалгебра

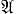
(F, k, n) = F[х₁, ..., х_k ]/М_n,

где F[х₁, ..., х_k ] - свободная алгебра с конечным числом образующих x_i над полем F характеристики нуль, а М_n - определенный выше Т-идеал тождеств матричной алгебры F_n . Алгебра 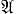(F, k, n) есть PI-A. без делителей нуля, она обладает классич. телом частных D(F, k, n), конечномерным над своим центром Z. Пусть, далее, (F_n)_k - пространство, элементами к-рого являются строки длины k, состоящие из матриц алгебры F_n . Можно говорить о нулях элементов алгебры 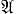(F, k, n), лежащих в пространстве (F_n)_k, об алгебраич. многообразиях пространства (F_n)_k и т. д. При этом окажутся выполненными основные положения классической алгебраич. геометрии. Так, имеет место некоммутативный аналог Гильберта теоремы о нулях. Неприводимым алгебраич. многообразиям соответствуют первичные идеалы алгебры, удовлетворяющие условию нётеровости. Выполняется теорема Крулля о совпадении максимальной из длин цепочек первичных идеалов алгебры 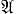(F, k, n) со степенью трансцендентности Z над F, к-рая в рассматриваемом случае равна

kn² - (n² - 1).

По аналогии с ассоциативными алгебрами можно определить с помощью элементов свободных алгебр PI-A. в других классах алгебр, обладающих свободными алгебрами (лиевы, альтернативные и др.).

Алгебра Ли над полем нулевой характеристики, удовлетворяющая n-му тождеству Энгеля

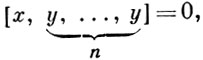
локально нильпотентна. Вопрос о том, влечет ли тождество Энгеля нильпотентность (проблема Xиггинса), решен положительно лишь для n = 4. Для полей положительной характеристики эта проблема имеет отрицательное решение.

Лит. : [1] Рrосеsi С., Rings with polynomical identities, N. Y., 1973; [2] Джекобсон H., Строение колец, пер. с англ., М., 1961; [3] Xерстейн И., Некоммутативные кольца, пер. с англ., М., 1972; [4] Кон П., Универсальная алгебра, пер. с англ., М., 1968; [5] Ширшов А. И., «Матем. сб. », 1957, т. 43 [85], вып. 2, с. 277-83; [6] Кострикин А. И., «Известия АН СССР. Сер. матем. », 1959, т. 23, № 1, с. 3-34; [7] Higman G., «Рrос. Cambr. Phil. Soc. », 1956 v. 52, part 1, p. 1-4; [8] Higgins P. J., «Рrос. Cambr. Phil. Soc. », 1954, t. 50, part 1, p. 8-15.

В. H. Латышев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.