С*-АЛГЕБРА

Расстановка ударений: С*-А`ЛГЕБРА

С*-АЛГЕБРА - банахова алгебра А над полем комплексных чисел, снабженная такой инволюцией, x → x^*, х ∈ А, что норма и инволюция связаны соотношением ||х^* х|| = ||x||² для любого элемента х ∈ А. С^*-А. были введены в 1943 (см. [1]) под назв. вполне регулярных колец, их наз. также B^*-алгебрами.

Важнейшие примеры С^*-А. 1) Алгебра С₀ (Х) непрерывных комплекснозначных функций на локально компактном хаусдорфовом пространстве X, стремящихся к нулю на бесконечности (т. е. таких непрерывных функций f на X, что для любого ε > 0 множество точек х ∈ Х, удовлетворяющих условию |f(x)| ≥ ε, компактно в X); С₀ (Х) снабжается равномерной нормой

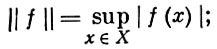
инволюция в С₀ (Х) определяется как переход к комплексно сопряженной функции: f^* (x) = f¯ (х). Любая коммутативная С^*-А. А изометрически и симметрически изоморфна С^*-А. (т. е. изоморфна как банахова алгебра А с инволюцией) С₀ (Х), где X - пространство максимальных идеалов алгебры А, снабженное топологией Гельфанда (см. [1], [2], [3]).

2) Алгебра L(Н) всех ограниченных линейных операторов в гильбертовом пространстве Н, рассматриваемая относительно обычных линейных операций и умножения операторов; инволюция в L(Н) определяется как переход к сопряженному оператору, норма - как обычная норма оператора.

Подмножество M ⊂ A наз. самосопряженным, если М = М^*, где М^* = {х^*, х ∈ М}. Любая замкнутая самосопряженная подалгебра В С^*-А. А является С^*-А. относительно линейных операций, умножения, инволюции и нормы, заимствованных из А; В наз. С^*-подалгеброй А. Всякая С^*-А. изометрически и симметрически изоморфна С^*-подалгебре нек-рой С^*-А. вида L(Н). Любой замкнутый двусторонний идеал I в С^*-А. А самосопряжен (поэтому I есть С^*-подалгебра А), факторалгебра A/I, снабженная естественными линейными операциями, умножением, инволюцией и нормой факторпространства, есть С^*-А. Множество К(Н) вполне непрерывных линейных операторов в гильбертовом пространстве Н есть замкнутый двусторонний идеал в L(H). Если А есть С^*-А., Ã - алгебра с инволюцией, получаемая из А присоединением единичного элемента, то на Ã существует единственная норма, превращающая Ã в С^*-А. и продолжающая норму на А. Кроме того, для С^*-А. определены операции ограниченной прямой суммы и тензорного произведения (см. [3], [4]).

Как и во всякой симметрияной банаховой алгебре, в С^*-А. А можно выделить подмножества: действительное линейное пространство А_h эрмитовых элементов; множество нормальных элементов; мультипликативную группу U унитарных элементов (если А содержит единичный элемент); множество А + положительных элементов. Множество А⁺ есть замкнутый конус в A_h, А⁺ ∪ (- А)⁺ = {0}, А⁺ - А⁺ = A_h, и конус А⁺ превращает А_h в упорядоченное действительное векторное пространство. Если А содержит единичный элемент 1. то 1 - внутренняя точка конуса A⁺ ⊂ A_h . Линейный функционал на А наз. положительным, если f(x) ≥ 0 для всех х ∈ А⁺ ; такой функционал непрерывен. Если х ∈ В, где В есть С^*-подалгебра А, то спектр элемента х в В совпадает со спектром х в А. Спектр эрмитова элемента действителен, спектр унитарного элемента лежит на единичной окружности, спектр положительного элемента неотрицателен. Построено функциональное исчисление для нормальных элементов С^*-А. Любая С^*-А. А имеет аппроксимативную единицу, лежащую в единичном шаре алгебры А и образованную положительными элементами из А. Если I, J - замкнутые двусторонние идеалы в А, то I + J - замкнутый двусторонний идеал в А и (I + J)⁺ = I⁺ + J⁺, Если I - замкнутый двусторонний идеал в J, J - замкнутый двусторонний идеал в А, то I - замкнутый двусторонний идеал в А. Всякий замкнутый двусторонний идеал есть пересечение содержащих его двусторонних примитивных идеалов; всякий замкнутый левый идеал в А - есть пересечение содержащих его максимальных регулярных левых идеалов.

Любой ^*-изоморфизм С^*-А. является изометрическим. Любой ^*-гомоморфизм π банаховой алгебры с инволюцией В в С^*-А. А непрерывен и ||π (x)|| ≤ ||x|| для всех х ∈ В. В частности, все представления банаховой алгебры с инволюцией (т. е. ^*-гомоморфизм В в С^*-А. вида L(Н)) непрерывны. Теория представлений С^*-А. составляют существенную часть теории С^*-А., и приложения теории С^*-А. связаны именно с теорией представлений С^*-А. Свойства представлений С^*-А. позволяют построить для каждой С^*-А. А топологич. пространство Â, наз. спектром С^*-А., и снабдить это пространство Макки борелевской структурой. Спектр С^*-А., вообще говоря, не удовлетворяет никаким аксиомам отделимости, но является локально бикомпактным Бэра пространством.

С^*-А. А наз. CCR-aлгеброй (соответственно GCR-алгеброй), если для любого ненулевого неприводимого представления π С^*-А. А в гильбертовом пространстве Н выполняется соотношение π (А) = K(Н_π) (соответственно π (A) ⊃ K(Н_π)).

С^*-А. наз. NGCR-алгеброй, если А не содержит ненулевых замкнутых двусторонних GСR-идеалов (т. е. идеалов, являющихся GСR-алгебрами). Любая С^*-А. А содержит максимальный двусторонний GCR-идеал I, и факторалгебра А/I есть АGСR-алгебра. Всякая GСR-алгебра содержит возрастающее семейство замкнутых двусторонних идеалов I_α, занумерованных порядковыми числами α, α ≤ ρ, такое, что I_ρ = А, I₁ = {0}, I_{α + 1} /I_α есть ССR-алгебра при всех α < ρ, и I_α = ∪_{α ' < α} I_{α '} для предельных порядковых чисел α. Спектр GCR-алгебры содержит открытое всюду плотное отделимое локально бикомпактное подмножество.

С^*-А. А наз. С^*-алгеброй типа I, если для любого представления π С^*-А. А в гильбертовом пространстве H_π Неймана алгебра, порожденная семейством π (А) в Н_π, есть алгебра Неймана типа I. Для С^*-А. А следующие условия эквивалентны: а) А есть С^*-А. типа I; б) А есть GСR-алгебра; в) любое факторпредставление С^*-А. А кратно неприводимому. Если А удовлетворяет этим условиям, то: 1) неприводимые представления С^*-А. А эквивалентны тогда и только тогда, когда их ядра совпадают; 2) спектр С^*-А. А есть T₀ - пространство. Если А - сепарабельная С^*-А., то каждое из условий 1) и 2) эквивалентно условиям а)-в). В частности, всякая сепарабельная С^*-А., имеющая единственное с точностью до эквивалентности неприводимое представление, изоморфна С^*-А. K(H) для нек-рого гильбертова пространства Н.

Пусть А есть С^*-А., Р - множество таких элементов х ∈ А, что функция π → Trπ (х) конечна и непрерывна на спектре С^*-А. А. Если линейная оболочка множества Р всюду плотна в А, то А наз. С^*-А. с непрерывным следом. Спектр таких С^*-А. отделим, и при нек-рых дополнительных условиях С^*-А. с непрерывным следом можно представить в виде алгебры вектор-функций на спектре А (см. [3]).

Пусть А есть С^*-A., F - множество положительных линейных функционалов на A с нормой ≤ 1, Р (А) - множество ненулевых крайних точек выпуклого множества F. Тогда Р(А) - множество чистых состояний С^*-А. А (см. Представления симметричных алгебр). Пусть В есть С^*-подалгебра А. Если А есть GСR-алгебра и В разделяет точки множества Р(А) ∪ {0}, т. е. для любых f₁, f₂ ∈ P(A) ∪ {0}, f₁ ≠ f₂, существует х ∈ В такой, что f₁ (x) ≠ f₂ (x), то В = А (теорема Стоуна-Вейерштрасса). Если А - произвольная С^*-А. и В разделяет точки множества Р¯ (A) ∪ {0}, то В = А.

Второе сопряженное пространство А^** с С^*-А. А естественным образом снабжается операцией умножения, превращающей А^** в С^*-А., изоморфную нек-рой алгебре Неймана; эта алгебра наз. обертывающей алгеброй Неймана С^*-А. (см. [3], [4]).

Теория С^*-А. имеет многочисленные применения в теории представлений групп и симметричных алгебр [3], теории динамич. систем [4], статистич. физике и квантовой теории поля [5], а также в теории операторов в гильбертовом пространстве [6].

Лит. : [1] Гельфанд И. М., Наймарк М. А., «Матем. сб. », 1943, т. 12, № 2, с. 197-213; [2] Наймарк М. А., Нормированные кольца, М., 1956; [3] Диксмье Ж., С^*-алгебры и их представления, пер. с франц., М., 1974-[4] Sakаi S., C^*-algebras and W^*-algebras, N. Y., 1971; [5] Рюэль Д., Статистическая механика. Строгие результаты, пер. с франц., М., 1971; [6] Dоuglas R. G., Banach Algebra Technigues in Operator Theory, N. Y., 1972.

А. И. Штерн.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.