
АКСИОМАТИЧЕСКИЙ МЕТОД
Расстановка ударений: АКСИОМАТИ`ЧЕСКИЙ МЕ`ТОД
АКСИОМАТИЧЕСКИЙ МЕТОД - способ построения научной теории, при к-ром в основу теории кладутся нек-рые исходные положения, наз. аксиомами теории, а все остальные предложения теории получаются как логич. следствия аксиом.
В математике А. м. зародился в работах древнегреческих геометров. Блестящим, остававшимся единственным вплоть до 19 в. образцом применения А. м. была геометрич. система, известная под назв. «Начал» Евклида (ок. 300 до н. э.). Хотя в то время не вставал еще вопрос об описании логич. средств, применяемых для извлечения содержательных следствий из аксиом, в системе Евклида уже достаточно четко проведена идея получения всего основного содержания геометрич. теории чисто дедуктивным путем из нек-рого, относительно небольшого, числа утверждений - аксиом, истинность к-рых представлялась наглядно очевидной.
Открытие в нач. 19 в. неевклидовой геометрии Н. И. Лобачевским и Я. Больяй (J. Bolyai) явилось толчком к дальнейшему развитию А. м. Они установили, что, заменив привычный и, казалось бы, единственно «объективно истинный» V постулат Евклида о параллельных его отрицанием, можно развивать чисто логич. путем геометрич. теорию, столь же стройную и богатую содержанием, как и геометрия Евклида. Этот факт заставил математиков 19 в. обратить специальное внимание на дедуктивный способ построения математич. теорий, что повлекло за собой возникновение новой проблематики, связанной с самим понятием А. м., и формальной (аксиоматической) математич. теории. По мере того как накапливался опыт аксиоматич. изложения математич. теорий - здесь надо отметить прежде всего завершение логически безупречного (в отличие от «Начал» Евклида) построения элементарной геометрии [М. Паш (М. Pasch), Дж. Пеано (G. Реаnо), Д. Гильберт (D. Hilbert)] и первые попытки аксиоматизации арифметики (Дж. Пеано), - уточнялось понятие формальной аксиоматич. системы (см. ниже); возникала специфич. проблематика, на основе к-рой выросла так наз. доказательств теория как основной раздел современной математич. логики.
Понимание необходимости обоснования математики и конкретные задачи в этой области зародились в более или менее отчетливой форме уже в 19 в. При этом, с одной стороны, уточнение основных понятий и сведение более сложных понятий к простейшим на точной и логически все более строгой основе проводились гл. обр. в области анализа [«ε - δ » - язык О. Коши (A. Cauchy), теоретико-функциональные концепции Б. Больцано (В. Bolzano) и К. Вейерштрасса (К. Weierstrass), континуум Г. Кантора (G. Cantor) и Р. Дедекинда (R. Dedekind)]; с другой стороны, открытие неевклидовых геометрий стимулировало развитие А. м., возникновение новых идей и постановку проблем более общего метаматематич. характера, прежде всего проблем, связанных с понятием произвольной аксиоматич. теории, таких, как проблемы непротиворечивости, полноты и независимости той или иной системы аксиом. Первые результаты в этой области принес метод интерпретаций, к-рый грубо может быть описан следующим образом. Пусть каждому исходному понятию и отношению данной аксиоматич. теории Т поставлен в соответствие нек-рый конкретный математич. объект. Совокупность таких объектов наз. полем интерпретации. Всякому утверждению 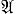 теории Т естественным образом ставится теперь в соответствие нек-рое высказывание
теории Т естественным образом ставится теперь в соответствие нек-рое высказывание 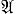 * об элементах поля интерпретации, к-рое может быть истинным или ложным. Тогда говорят, что утверждение
* об элементах поля интерпретации, к-рое может быть истинным или ложным. Тогда говорят, что утверждение 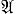 теории Т, соответственно, истинно или ложно в данной интерпретации. Поле интерпретации и его свойства сами обычно являются объектом рассмотрения к.-л., вообще говоря другой, математич. теории Т1, к-рая, в частности, тоже может быть аксиоматической. Метод интерпретаций следующим образом позволяет устанавливать факт относительной непротиворечивости, т. е. доказывать суждения типа: «если теория Т1 непротиворечива, то непротиворечива и теория Т». Пусть теория Т проинтерпретирована в теории Т1 таким образом, что все аксиомы Аi теории Т интерпретируются истинными суждениями А*i теории Т1 . Тогда всякая теорема теории Т, т. е. всякое утверждение А, логически выведенное из аксиом Аi в Т, интерпретируется в Тх нек-рым утверждением А*, выводимым в Т1 из интерпретаций А*i аксиом Аi, и, следовательно, истинным. Последнее утверждение опирается на еще одно неявно делаемое нами допущение известного подобия логич. средств теорий Т и Т1, но практически это условие обычно выполняется. (На заре применения метода интерпретаций об этом допущении специально даже не задумывались: оно представлялось само собой разумеющимся; на самом деле в случае первых опытов доказательства теорем об относительной непротиворечивости логич. средства теорий Т и Т1 просто совпадали - это была классич. логика предикатов.) Пусть теперь теория Т противоречива, т. е. нек-рое утверждение А этой теории выводимо в ней вместе со своим отрицанием. Тогда из вышесказанного следует, что утверждения А* и «не А* » будут одновременно истинными утверждениями теории Т1, т. е., ято теория Т1 противоречива. Этим методом была, напр., доказана [Ф. Клейн (F. Klein), А. Пуанкаре (Н. Poincaré)] непротиворечивость неевклидовой геометрии Лобачевского в предположении, что непротиворечива геометрия Евклида; а вопрос о непротиворечивости гильбертовой аксиоматизации евклидовой геометрии был сведен (Д. Гильберт) к проблеме непротиворечивости арифметики. Метод интерпретаций позволяет также решать вопрос о независимости систем аксиом: для доказательства того, что аксиома А теории Т не зависит от остальных аксиом этой теории, т. е. не выводима из них, и, следовательно, существенно необходима для получения всего объема данной теории, достаточно построить такую интерпретацию теории Т, в к-рой аксиома А была бы ложна, а все остальные аксиомы этой теории истинны. Иной формой этого способа доказательства независимости А является установление непротиворечивости теории, к-рая получается, если в данной теории Т аксиому А заменить ее отрицанием. Упомянутое выше сведение проблемы непротиворечивости геометрии Лобачевского к проблеме непротиворечивости евклидовой геометрии, а этой последней - к вопросу о непротиворечивости арифметики имеет своим следствием утверждение, что V постулат Евклида не выводим из остальных аксиом геометрии, если только непротиворечива арифметика натуральных чисел. Слабая сторона метода интерпретаций состоит в том, что в вопросах непротиворечивости и независимости систем аксиом он дает возможность получать результаты, носящие неизбежно лишь относительный характер. Но важным достижением этого метода стал тот факт, что с его помощью была выявлена на достаточно точной основе особая роль арифметики как такой математич. теории, к вопросу о непротиворечивости к-рой сводится аналогичный вопрос для целого ряда других теорий.
теории Т, соответственно, истинно или ложно в данной интерпретации. Поле интерпретации и его свойства сами обычно являются объектом рассмотрения к.-л., вообще говоря другой, математич. теории Т1, к-рая, в частности, тоже может быть аксиоматической. Метод интерпретаций следующим образом позволяет устанавливать факт относительной непротиворечивости, т. е. доказывать суждения типа: «если теория Т1 непротиворечива, то непротиворечива и теория Т». Пусть теория Т проинтерпретирована в теории Т1 таким образом, что все аксиомы Аi теории Т интерпретируются истинными суждениями А*i теории Т1 . Тогда всякая теорема теории Т, т. е. всякое утверждение А, логически выведенное из аксиом Аi в Т, интерпретируется в Тх нек-рым утверждением А*, выводимым в Т1 из интерпретаций А*i аксиом Аi, и, следовательно, истинным. Последнее утверждение опирается на еще одно неявно делаемое нами допущение известного подобия логич. средств теорий Т и Т1, но практически это условие обычно выполняется. (На заре применения метода интерпретаций об этом допущении специально даже не задумывались: оно представлялось само собой разумеющимся; на самом деле в случае первых опытов доказательства теорем об относительной непротиворечивости логич. средства теорий Т и Т1 просто совпадали - это была классич. логика предикатов.) Пусть теперь теория Т противоречива, т. е. нек-рое утверждение А этой теории выводимо в ней вместе со своим отрицанием. Тогда из вышесказанного следует, что утверждения А* и «не А* » будут одновременно истинными утверждениями теории Т1, т. е., ято теория Т1 противоречива. Этим методом была, напр., доказана [Ф. Клейн (F. Klein), А. Пуанкаре (Н. Poincaré)] непротиворечивость неевклидовой геометрии Лобачевского в предположении, что непротиворечива геометрия Евклида; а вопрос о непротиворечивости гильбертовой аксиоматизации евклидовой геометрии был сведен (Д. Гильберт) к проблеме непротиворечивости арифметики. Метод интерпретаций позволяет также решать вопрос о независимости систем аксиом: для доказательства того, что аксиома А теории Т не зависит от остальных аксиом этой теории, т. е. не выводима из них, и, следовательно, существенно необходима для получения всего объема данной теории, достаточно построить такую интерпретацию теории Т, в к-рой аксиома А была бы ложна, а все остальные аксиомы этой теории истинны. Иной формой этого способа доказательства независимости А является установление непротиворечивости теории, к-рая получается, если в данной теории Т аксиому А заменить ее отрицанием. Упомянутое выше сведение проблемы непротиворечивости геометрии Лобачевского к проблеме непротиворечивости евклидовой геометрии, а этой последней - к вопросу о непротиворечивости арифметики имеет своим следствием утверждение, что V постулат Евклида не выводим из остальных аксиом геометрии, если только непротиворечива арифметика натуральных чисел. Слабая сторона метода интерпретаций состоит в том, что в вопросах непротиворечивости и независимости систем аксиом он дает возможность получать результаты, носящие неизбежно лишь относительный характер. Но важным достижением этого метода стал тот факт, что с его помощью была выявлена на достаточно точной основе особая роль арифметики как такой математич. теории, к вопросу о непротиворечивости к-рой сводится аналогичный вопрос для целого ряда других теорий.
Дальнейшее развитие - а в известном смысле это была вершина - А. м. получил в работах Д. Гильберта и его школы в виде так наз. метода формализма в основаниях математики. В рамках этого направления была выработана следующая стадия уточнения понятия аксиоматич. теории, а именно понятие формальной системы. В результате этого уточнения оказалось возможным представлять сами математич. теории как точные математич. объекты и строить общую теорию, или метатеорию, таких теорий. При этом соблазнительной представлялась перспектива (и Д. Гильберт был в свое время ею увлечен) решить на этом пути все главные вопросы обоснования математики. Основным понятием этого направления является понятие формальной системы. Всякая формальная система строится как точно очерченный класс выражений - формул, в к-ром нек-рым точным образом выделяется подкласс формул, наз. теоремами данной формальной системы. При этом формулы формальной системы непосредственно не несут в себе никакого содержательного смысла, и их можно строить из произвольных, вообще говоря, значков или элементарных символов, руководствуясь только соображениями технического удобства. На самом деле способ построения формул и понятие теоремы той или иной формальной системы выбираются с таким расчетом, чтобы весь этот формальный аппарат можно было применять для выражения, возможно более адекватного и полного, той или иной конкретной математической (и не математической) теории, точнее, как ее фактич. содержания, так и ее дедуктивной структуры. Общая схема построения (задания) произвольной формальной системы S такова.
I. Язык системы S:
а) алфавит - перечень элементарных символов системы;
б) правила образования (синтаксис) - правила, по к-рым из элементарных символов строятся формулы системы S; при этом последовательность элементарных символов считается формулой тогда и только тогда, когда она может быть построена с помощью правил образования.
II. Аксиомы системы S. Выделяется нек-рое множество формул (обычно конечное или перечислимое), к-рые наз. аксиомами системы S.
III. Правила вывода системы S. Фиксируется (обычно конечная) совокупность предикатов R1, ..., Rk на множестве всех формул системы S. Пусть Ri (х1, ..., хni + 1) - к.-л. из этих предикатов (ni > 0); если для данных формул F1, ..., Fni + 1 утверждение Ri (F1, ..., Fni + 1) истинно, то говорят, что формула Fni + 1 непосредственно следует из формул F1, ..., Fni . по правилу Ri .
Заданием I, II, III исчерпывается задание формальной системы S как точного математич. объекта, поскольку понятие теоремы или выводимой формулы системы S образуется для всех формальных систем следующим единообразным способом (при этом степень точности определяется уровнем точности задания алфавита, правил образования и правил вывода, т. е. предикатов R1, ..., Rk). Выводом системы S наз. всякая конечная последовательность формул системы S, в к-рой каждая формула либо является аксиомой системы S, либо непосредственно следует из к.-л. предшествующих ей в этой последовательности формул по одному из правил вывода Ri системы S. Формула системы S наз. теоремой этой системы, если существует вывод системы S, заканчивающийся этой формулой.
Всякую конкретную математич. теорию Т можно перевести на язык подходящей формальной системы S таким образом, что каждое осмысленное (ложное или истинное) предложение теории Т выражается нек-рой формулой системы S.
Естественно было надеяться, что этот метод формализации позволит строить все положительное содержание математич. теорий на такой точной и, казалось бы, надежной основе, как понятие выводимой формулы (теоремы формальной системы), а такие принципиальные вопросы, как проблема непротиворечивости математич. теорий, решать в форме доказательств соответствующих утверждений о формализующих эти теории формальных системах. Поскольку формальные системы описанного выше типа сами оказываются точными, или, как говорили в школе Гильберта, финитными, математич. объектами, можно было ожидать, что удастся получить финитные доказательства утверждений о непротиворечивости, т. е. доказательства, к-рые в определенном смысле были бы эффективными, не зависящими от тех мощных средств, вроде абстракции актуальной бесконечности, к-рые в классических математич. теориях как раз и являются причиной трудностей в их обосновании. Таким образом, требование финитности средств, применяемых для получения результатов о формальных системах, в частности теорем о их непротиворечивости, было вполне закономерной особенностью формалистич. программы Гильберта. Однако результаты К. Гёделя (К. Godel) начала 30-х гг. 20 в. привели к краху основных надежд, связывавшихся с этой программой. Гёдель показал:
1) Всякая естественная, непротиворечивая формализация S арифметики или любой другой математич. теории, содержащей арифметику (напр., теории множеств), неполна и непополнима в том смысле, что: а) в S имеются (содержательно истинные) неразрешимые формулы, т. е. такие формулы А, что ни А, ни отрицание А не выводимы в S (неполнота формализованной арифметики), б) каким бы конечным множеством дополнительных аксиом (напр., неразрешимыми в S формулами) ни расширить систему S, в новой, усиленной таким образом, формальной системе неизбежно появятся свои неразрешимые формулы (непополнимость; см. [5], а также Гёделя теорема о неполноте).
2) Если формализованная арифметика в действительности непротиворечива, то хотя утверждение о ее непротиворечивости выразимо на ее собственном языке, однако доказательство этого утверждения, проведенное средствами, формализуемыми в ней самой, невозможно.
Это означает, что уже для арифметики принципиально невозможно исчерпать весь объем ее содержательно истинных суждений классом выводимых формул какой бы то ни было формальной системы, и что нет никакой надежды получить когда-либо финитное доказательство непротиворечивости арифметики, т. к., по-видимому, всякое разумное уточнение понятия финитного доказательства оказывается формализуемым в формальной арифметике.
Все это ставит определенные границы возможностям Д. м. в том его виде, к-рый он приобрел в рамках гильбертовского формализма. Однако и в этих границах он сыграл и продолжает играть важную роль в основаниях математики. Так, напр., уже после описанных результатов Гёделя им же в 1938-40, а затем П. Коэном (P. Cohen) в 1963 на основе аксиоматич. подхода с применением метода интерпретаций были получены фундаментальные результаты о совместимости и независимости аксиомы выбора и континуум-гипотезы в теории множеств (см. [6], [7]). Что касается такого основного вопроса оснований математики, как проблема непротиворечивости, то после результатов Гёделя стало ясно, что для его решения, по-видимому, не обойтись без других, отличных от финитистских, средств и идей. Здесь оказались возможными разные подходы, не для всех математиков в равной степени приемлемые или убедительные, в частности в виду существования различных точек зрения на допустимость тех или иных логич. средств. Из результатов о непротиворечивости формальных систем следует прежде всего указать на доказательство непротиворечивости формализованной арифметики (см. [8]), к-рое опирается на бесконечную индукцию до нек-рого счетного трансфинита. Другим, более поздним, примером такого рода является попытка обоснования утверждения о непротиворечивости формальной системы анализа с помощью нек-рых идей интуиционизма (см. [9]).
Лит. : [1] «Начала» Евклида, пер. с греч., кн. 1-15, М. - Л., 1948-50; [2] Каган В. Ф., Основания геометрии, ч. 1, М. - Л., 1949; [3] Гильберт Д., Основания геометрии, пер. с нем., М. - Л., 1948; [4] Реаnо G., «Rivista di matematica», 1891, v. 1, p. 1-10; [5] Gödel K., «Monatsh. Math. Phys. », 1931, Bd 38, S. 173-98; [6] Гёдель К., «Успехи матем. наук», 1948, т. 3, в. 1, с. 96-149; [7] Коэн П. Дж., Теория множеств и континуум-гипотеза, пер. с англ., М., 1969; [8] Генцен Г., Непротиворечивость чистой теории чисел, в кн. : Математическая теория логического вывода, М., 1967, с. 77-153; [9] Sреctor С., в кн. : Recursive function theory, Providence, 1962, p. 1-27.
П. С. Новиков.
Источники:
- Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'