АКСИОМАТИЗИРУЕМЫЙ КЛАСС

Расстановка ударений: АКСИОМАТИЗИ`РУЕМЫЙ КЛА`СС

АКСИОМАТИЗИРУЕМЫЙ КЛАСС - класс однотипных моделей, определяемый системой аксиом. Класс K моделей формального языка L наз. аксиоматизируемым (конечно аксиоматизируемым), если существует (конечная) система ∑ замкнутых формул языка L такая, что K содержит те и только те модели, на к-рых определены и истинны все формулы из ∑ (см. Алгебраическая система). Класс моделей рекурсивной сигнатуры наз. рекурсивно аксиоматизируемым, если он может быть задан рекурсивным множеством аксиом.

Многие классы алгебраич. систем, изучаемых в математике, определяются системой аксиом языка 1-й ступени. Напр., классы всех булевых алгебр, всех групп, всех полей, всех решеток являются конечно аксиоматизируемыми. Классы всех групп без кручения, всех полей характеристики 0, всех алгебраически замкнутых полей рекурсивно аксиоматизируемы, хотя не конечно аксиоматизируемы. Теория А. к. выявляет закономерности, общие для всех классов объектов, определяемых с помощью данного языка; она хорошо разработана для языка 1-й ступени, поэтому далее речь идет только о таких классах и формулах.

Две модели наз. элементарно эквивалентными, если всякая формула языка 1-й ступени, истинная в одной из них, истинна и в другой. Модель 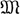наз. элементарным расширением модели 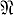, если всякая формула, определенная и истинная в 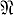, будет истинной в .

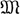Элементарно замкнутый класс К моделей наз. полным, если все его модели элементарно эквивалентны между собой. Каждый А. к. моделей является суммой попарно непересекающихся полных классов. Класс наз. категоричным в мощности m, если все его модели мощности m изоморфны. Полный класс моделей счетной сигнатуры, категоричный в несчетной мощности, будет категоричным во всех несчетных мощностях, но может быть некатегоричным в счетной мощности; и в этом случае класс имеет счетное число попарно неизоморфных счетных моделей. Для любого n ≠ 2 существует полный А. к., имеющий ровно n неизоморфных счетных моделей.

А. к. моделей К наз. разрешимым, если существует алгорифм, позволяющий для каждой замкнутой формулы языка L указать, истинна или нет она на каждой модели К. Связь полных, категоричных и разрешимых классов дает теорема: если К категоричен в бесконечной мощности и не имеет конечной модели, то он полон. Полный рекурсивно А. к. моделей разрешим.

Обобщениями А. к. являются редукционные классы и проективные классы. Проективные классы определяются аксиомой 2-й ступени, имеющей вид:

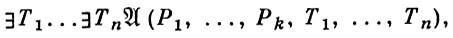
где Р_i, Т_i - предикатные переменные, 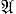(P₁, ..., P_k, T₁, ..., T_n) - формула сигнатуры σ = (Р₁, ..., P_k, T₁, ..., T_n). Многие свойства А. к. переносятся на эти классы.

Лит. : [1] Мальцев А. И., Алгебраические системы, М., 1970; [2] его же, в кн. : Тр. 4-го Всесоюзн. матем. съезда, т. 1, Л., 1963, с. 169-98.

А. Д. Тайманов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.