АЗАРТНАЯ ИГРА

Расстановка ударений: АЗА`РТНАЯ ИГРА`

АЗАРТНАЯ ИГРА - многошаговая игра одного игрока. А. и. G определяют как систему

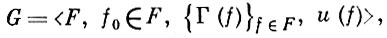
где F - множество капиталов, f₀ - начальный капитал игрока, Г(f) - множество конечно аддитивных мер, определенных на всех подмножествах F, u(f) - функция полезности (см. Полезности теория) игрока, определенная на множестве его капиталов. Игрок выбирает σ₀ ∈ Г(f₀), и его капитал f₁ будет распределен согласно мере σ₀ . Затем игрок выбирает σ₁ (f₁) ∈ Г(f₁) и получает соответственно f₂ и т. д. Последовательность σ = {σ₀, σ₁,...} является стратегией игрока. Если игрок кончает игру в момент t, то его выигрыш определяется как математич. ожидание по о функции u(f_t). Цель игрока состоит в максимизации его функции полезности. Простейшим примером А. и. является лотерея. Игрок, имея наличный капитал f, может приобрести k лотерейных билетов стоимостью с, k = 1, ..., [f/с]. Каждому к соответствует вероятностная мера на множестве всех капиталов, и после тиража капитал игрока становится равным f₁ . Если f₁ < c, то игра кончается; если f₁ > c, то игрок может либо выйти из игры, либо снова приобретать лотерейные билеты в количестве от одного до [f₁ /с] штук и т. д. Функцией полезности игрока может являться, напр., математич. ожидание капитала или вероятность получения выигрыша не менее определенной величины.

Теория А. и. является составной частью общей теории управляемых вероятностных процессов. В А. и. могут играть и сразу несколько лиц, но с теоретико-игровой точки зрения А. и. - игра одного игрока, т. к. его выигрыш не зависит от стратегий партнеров.

Лит. : [1] Dubins L. Е., Savage L. J., How to gamble if you must: Inequalities for stochastic processes, N. Y. - [a. o.], 1965.

E. Б. Яновская.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.