l-АДИЧЕСКИЕ КОГОМОЛОГИИ

Расстановка ударений: l-АДИ`ЧЕСКИЕ КОГОМОЛО`ГИИ

l-АДИЧЕСКИЕ КОГОМОЛОГИИ - одна из конструкций когомологий абстрактных алгебраич. многообразии и схем. Этальные когомологии схем являются периодич. модулями. Для различных нужд, в первую очередь для доказательства формулы Лефшеца и приложений к дзета-функциям, необходимы когомологии «с коэффициентами в кольцах нулевой характеристики». Они получаются из этальных когомологий переходом к проективному пределу.

Пусть l - простое число, l-адическим пучком на схеме А наз. проективная система F = (F_n)_{n ∈ N} этальных абелевых пучков F_n такая, что для всех n гомоморфизмы перехода F_{n + 1} → F_n эквивалентны канонич. морфизму F_{n + 1} → F_{n + 1} /lⁿ F_{n + 1} . Каждая компонента F_n Z-адического пучка является пучком Z/lⁿ Z-модулей. l-адический пучок F наз. конструктивным (соответственно, локально постоянным), если все пучки Fⁿ конструктивные (локально постоянные) этальные пучки. Имеет место естественная эквивалентность категории локально постоянных конструктивных пучков на связной схеме X и категорией модулей конечного типа над кольцом Z_l целых Z-адических чисел, на к-рых непрерывно слева действует фундаментальная группа схемы X. Это показывает, что конструктивные локально постоянные пучки являются абстрактными аналогами системы локальных коэффициентов в топологии. Примерами конструктивных Z-адических пучков являются пучок Z_{l, X} = ((Z/lⁿ Z)x)_{n ∈ N}, пучки Тейтa 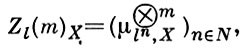где (Z/lⁿ Z)_X - постоянный пучок на X, ассоциированный с группой Z/lⁿ Z, а μ_{lⁿ, X} - пучок корней lⁿ-й степени из единицы на X. Если А - абелева схема над X, то T_l (A) = (A_lⁿ)_{n ∈ N}, где A_lⁿ - ядро умножения в А на lⁿ, образует локально постоянный конструктивный Z-адический пучок на X, наз. модулем Тейта Целевой схемы А.

Если X - схема над полем k, X a X¯ = X⊗_k k¯_s - схема, полученная из X заменой базы с А: на сепарабельное замыкание k¯_s поля k, и F = (F_n) - Z-адический пучок на X, то этальные когомологии Hⁱ (Х¯, F¯_n) определяют проективную систему (Нⁱ (Х¯, F¯_n))_{n ∈ N} Gal(k¯_s /k)-модулей. Проективный предел Нⁱ (Х¯, F) = 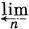Нⁱ (Х¯, F¯_n) естественным образом снабжается структурой Z_l-модуля, на к-ром Gal(k¯_s /k) действует непрерывно относительно Z-адической топологии, и наз. i-ми l-адическими когомологиями пучка F на А. В случае, когда k = k¯_s, обычно пишут Нⁱ (Х¯, F) = Hⁱ (X, F). На l-A. к. конструктивных Z-адических пучков переносятся фундаментальные теоремы об этальных когомологиях. Если Q_l - поле рациональных l-адических чисел, то (Q_l-пространства Hⁱ_l (Х¯) = = Нⁱ (Х¯, Z_l)⊗ Q_l наз. рациональными Z-адическими когомологиями схемы А. Их размерность b_i (X; l) (в случае, когда она определена) наз. i-м числом Бетти А. Для полных k-схем числа b_i (Х; l) определены и не зависят от l(l ≠ char k). Если k - алгебраически замкнутое поле характеристики р и l ≠ p, то сопоставление гладкому полному k-многообразию пространств Hⁱ_l (X) определяет Вейля когомологии. В случае, когда k = С - поле комплексных чисел, имеет место теорема сравнения: Hⁱ_l = Hⁱ (X, Q)⊗ Q_l .

Лит. : [1] Grot̂hendieck А., в кн. : Seminare Bourbaki, Textes des conférences. Annee, 1964/65, N. Y. - Amst., 1966, exposes № 279, p. 1-15.

И. В. Долгачев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.