
АДИЧЕСКАЯ ТОПОЛОГИЯ
Расстановка ударений: АДИ`ЧЕСКАЯ ТОПОЛО`ГИЯ
АДИЧЕСКАЯ ТОПОЛОГИЯ - линейная топология кольца А, в к-рой фундаментальная система окрестностей нуля образована степенями  n нек-рого двустороннего идеала
n нек-рого двустороннего идеала  . В этом случае топология наз.
. В этом случае топология наз.  -адической, а идеал
-адической, а идеал  - идеалом определения топологии. Замыкание любого множества F ⊂ A в
- идеалом определения топологии. Замыкание любого множества F ⊂ A в  -адической топологии равно ∩n ≥ 0 (F +
-адической топологии равно ∩n ≥ 0 (F +  n); в частности, топология отделима тогда, и только тогда, когда ∩n ≥ 0
n); в частности, топология отделима тогда, и только тогда, когда ∩n ≥ 0 n = (0). Отделимое пополнение Â кольца А в
n = (0). Отделимое пополнение Â кольца А в  -адической топологии изоморфно проективному пределу
-адической топологии изоморфно проективному пределу 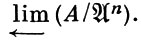 .
.
Аналогично определяется  -адическая топология A-модуля М: ее фундаментальная система окрестностей нуля задается подмодулями
-адическая топология A-модуля М: ее фундаментальная система окрестностей нуля задается подмодулями  n М; в
n М; в  -адической топологии М становится топологическим A-модулем.
-адической топологии М становится топологическим A-модулем.
Пусть A - коммутативное кольцо с единицей в  -адической топологии и Â - его пополнение; если
-адической топологии и Â - его пополнение; если  - идеал конечного типа, то топология в Â является
- идеал конечного типа, то топология в Â является 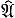 , а
, а 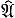 n =
n =  n Â. Если
n Â. Если  - максимальный идеал, то Â является локальным кольцом с максимальным идеалом
- максимальный идеал, то Â является локальным кольцом с максимальным идеалом  . Топологией локального кольца считается А. т., определяемая максимальным идеалом (m-адическая топология).
. Топологией локального кольца считается А. т., определяемая максимальным идеалом (m-адическая топология).
Для изучения А. т. колец фундаментальной является лемма Артина-Риса: пусть A есть коммутативное нётерово кольцо,  есть идеал в A, Е есть A-модуль конечного типа и F-подмодуль модуля Е. Тогда существует такое k, что для любого n ≥ 0 выполняется равенство
есть идеал в A, Е есть A-модуль конечного типа и F-подмодуль модуля Е. Тогда существует такое k, что для любого n ≥ 0 выполняется равенство
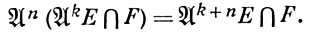
Топологич. интерпретация леммы Артина-Риса показывает, что  -адическая топология на F индуцирована
-адическая топология на F индуцирована  -адической топологией модуля Е. Отсюда следует, что пополнение Â кольца A в
-адической топологией модуля Е. Отсюда следует, что пополнение Â кольца A в  -адической топологии является плоским A-модулем (см. Плоский модуль), что пополнение Ê A-модуля Е конечного типа совпадает с Е⊕A Â, а также теорема Крулля:
-адической топологии является плоским A-модулем (см. Плоский модуль), что пополнение Ê A-модуля Е конечного типа совпадает с Е⊕A Â, а также теорема Крулля:  -адическая топология нётерова кольца отделима тогда, и только тогда, когда множество 1 +
-адическая топология нётерова кольца отделима тогда, и только тогда, когда множество 1 +  не содержит делителей нуля. В частности, топология отделима, если
не содержит делителей нуля. В частности, топология отделима, если  содержится в радикале (Джекобсона) кольца.
содержится в радикале (Джекобсона) кольца.
Лит. : [1] Зарисский О., Самюэль П., Коммутативная алгебра, пер. с англ., т. 2, М., 1963; [2] Бурбаки Н., Коммутативная алгебра, пер. с франц., М., 1971.
В. И. Данилов.
Источники:
- Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'