АДЕЛЬ

Расстановка ударений: АДЕ`ЛЬ

АДЕЛЬ - элемент группы аделей, т. е. топологич. прямого произведения

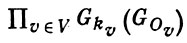
групп G_kv с отмеченными открытыми подгруппами GQ Здесь G_k- линейная алгебраическая группа, определенная над глобальным полем k, V - множество всех неэквивалентных нормирований поля k, k_v - пополнение к относительно v ∈ V, O_v - кольцо целых элементов в k_v . Группа А. алгебраич. группы G обозначается через G_A . Так как все группы G_kr локально компактны, a G_Ov компактны, то G_A - локально компактная группа.

Примеры. 1) Если G_k - аддитивная группа k⁺ поля k, то G_A обладает естественной структурой кольца, к-рое наз. кольцом аделей поля k и обозначается A_k . 2) Если G_k - мультипликативная группа k^* поля k, то G_k наз. группой иделей поля k (группа иделей является группой единиц в кольце аделей A_k). 3) Если G_k = GL(n, k) - полная линейная группа над k, то G_A состоит из таких элементов g = (g_v) ∈ П_{v ∈ V} G_v, что g_v ∈ GL(n, O_v) для почти всех нормирований v.

Понятие группы А. было впервые введено К. Шевалле (С. Chevalley) в 30-х гг. 20 в. для полей алгебраич. чисел в связи с потребностями теории полей классов. Спустя 20 лет оно было обобщено М. Кнезером (М. Kneser) и Ц. Тамагава (Т. Tamagawa) на алгебраич. группы (см. [1], [2]). Последние заметили, что основные результаты об арифметике квадратичных форм над числовыми полями удобно переформулировать на языке группы А.

Образ диагонального вложения G_k в G_A является дискретной подгруппой в G_A и наз. подгруппой главных аделей. Если ∞ - множество всех архимедовых нормирований k, то

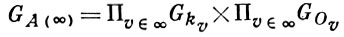
наз. подгруппой целых аделей. Если G_k = k^*, то число различных двойных классов смежности вида G_k xGA_(∞) группы A. G_A конечно и равно числу классов идеалов поля k. Естественно возникающий вопрос о конечности числа таких двойных классов для произвольной алгебраич. группы G связан с теорией приведения для подгруппы главных А., т. е. с конструкцией фундаментальной области для факторпространства G_A /G_k . В [5] доказано, что G_A /G_k тогда и только тогда компактно, когда группа G является k-анизотропной (см. Анизотропная группа). Более того, решен вопрос о том, когда над полем алгебраич. чисел факторпространство G_A /G_k имеет конечный объем в Хаара мере. Так как G_A локально компактна, то такая мера всегда существует и объем G_A /G_k в мере Хаара конечен тогда и только тогда, когда группа G не имеет рациональных k-характеров (см. Характер алгебраич. группы). Величина τ (G) объема G_A /G_k представляет важный арифметич. инвариант алгебраич. группы G (см. Тамагавы число). Опираясь на эти результаты, доказано (см. [5]), что для произвольной алгебраич. группы G имеет место разложение

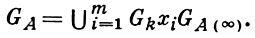
Для случая, когда k-функциональное поле, также доказана конечность числа двойных классов смежности указанного вида для группы А. алгебраич. группы и построен аналог теории приведения [6]. Относительно разнообразных арифметич. применений группы А. см. [4], [7].

Лит. : [1] Вейль А., «Математика», 1964, т. 8, №4, с. 3-74; [2] Арифметические группы и автоморфные функции пер. с англ. и франц., М., 1969, с. 44-55; [3] Алгебраическая теория чисел, пер. с англ., М., 1969; [4] Итоги науки. Алгебра. Геометрия. Топология, т. 11, М., 1973, с. 5-37; [5] Вorel А., в кн. : Publ. Math. I. H. E. S., 1963, № 16, р. 5-30; [6] Harder G., «Invent. math. », 1969, v. 7, № 1, p. 33-54; [7] Платонов В. П., «Труды матем. института им. Стеклова», 1973, т. 132, с. 162-68; [8] Вейль А., Основы теории чисел, пер. с англ., М., 1972.

В. П. Платонов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.