АДДИТИВНОЕ ОТНОШЕНИЕ

Расстановка ударений: АДДИТИ`ВНОЕ ОТНОШЕ`НИЕ

АДДИТИВНОЕ ОТНОШЕНИЕ - подмодуль r прямой суммы А⊕ B двух модулей А и В над нек-рым кольцом R. Каждое А. о. можно рассматривать, таким образом, и как (неоднозначное) отображение r : А → В, точнее как «многозначный» гомоморфизм, т. е. гомоморфизм r⁰ подмодуля Def r в фактормодуль B/Ind(r), где

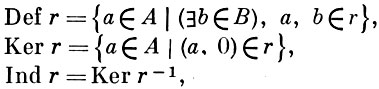
здесь r^{- 1} : В → А - обратное к А. о. r отношение, состоящее из всех таких пар (b, а) ∈ B⊕ A, что (а, b) ∈ r. Обратно, если даны подмодуль S ⊂ A, фактормодуль B/L модуля В и гомоморфизм β : S → B/L, то существует и притом единственное А. о. r : А → В такое, что г⁰ = β.

Если даны два А. о. r : А → В и s : В → С, то, как и для других бинарных отношений, может быть определено произведение А. о. sr: А → С (это множество всех пар (а, с) ∈ А⊕ С таких, что существует элемент b ∈ В, для к-рого (а, b) ∈ r и (b, c) ∈ s). Это умножение ассоциативно (там, где оно определено), более того, А. о. образуют категорию с инволюцией r → r^{- 1} .

А. о. используются для естественного определения связывающих гомоморфизмов для точных последовательностей комплексов. Аналогичные рассмотрения могут быть проведены не только в категории модулей, но и в любой абелевой категории.

Лит. : [1] Маклейн С, Гомология, пер. с англ., М., 1966; [2] Пуппе Д., «Математика», 1964, т. 8, № 6, с. 109-139.

А. В. Михалев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.