АДДИТИВНАЯ ТЕОРИЯ ЧИСЕЛ

Расстановка ударений: АДДИТИ`ВНАЯ ТЕО`РИЯ ЧИ`СЕЛ

АДДИТИВНАЯ ТЕОРИЯ ЧИСЕЛ - раздел теории чисел, в к-ром изучаются задачи о разложении целых чисел на слагаемые заданного вида, а также алгебраич. и геометрич. аналоги таких задач, относящиеся к полям алгебраич. чисел и к множествам точек решетки. Эти задачи наз. аддитивными задачами. Обычно рассматриваются аддитивные задачи о разложении больших чисел.

К классич. проблемам А. т. ч. относятся: задача о представлении числа суммой четырех квадратов, девяти кубов и т. д. (см. Варинга проблема); задача о представлении числа в виде суммы не более трех простых (см. Гольдбаха проблема); задача о представлении числа в виде суммы простого и двух квадратов (см. Харди-Литлвуда проблема) и другие аддитивные проблемы. Для решения задач А. т. ч. применяются аналитические, алгебраические, элементарные и смешанные методы, а также методы, основанные на вероятностных соображениях. В зависимости от методов решения, аддитивные задачи входят составной частью в другие разделы теории чисел - аналитич. теорию чисел, алгебраич. теорию чисел, вероятностную теорию чисел.

Первые систематич. результаты в А. т. ч. были получены Л. Эйлером (L. Euler, 1748), к-рый исследовал с помощью степенных рядов разложения целых чисел на положительные слагаемые; в частности, им была рассмотрена задача о разложении числа на заданное количество слагаемых.

Многие классич. задачи А. т. ч. решаются методом редукции к производящим функциям, к-рый восходит к Л. Эйлеру и лежит в основе аналитич. методов, развитых Г. X. Харди (G. Н. Hardy) и Дж. И. Литлвудом (J. Е. Littlewood) и И. М. Виноградовым. Исходной является идея сопоставления заданным последовательностям A_i = {a_i} (где а_i ≥ 0 - целое, i = 1, 2, 3,...) степенных рядов

с производящей функцией

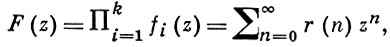
где r(n) = r_k, а(n) - количество представлений числа n в виде

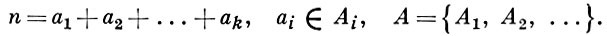
При этом r(n) вычисляется при помощи интеграла Коши. В методе Виноградова степенные ряды заменяются тригонометрич. суммами

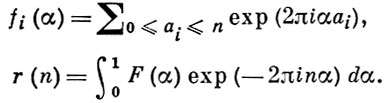
Из r(n) выделяется главная часть, состоящая из интервалов, распространенных на окрестности нек-рых рациональных точек. Вместо аналитич. свойств F(z), требующих в ряде задач А. т. ч. привлечения гипотез, аналогичных Римана гипотезе, центральную роль при вычислении r(n) играют чисто арифметич. оценки тригонометрич. сумм по методу Виноградова и законы распределения простых чисел в арифметич. прогрессиях, получаемые трансцендентными методами теории L-функций Дирихле. Устанавливается, что в зависимости от к либо r(n) ≠ 0 для всех n ≥ 1, либо r(n) ≠ 0 для достаточно больших n (n ≥ n₀ (А)), либо для почти всех n выполняется соотношение r(n) ≠ 0, т. е.

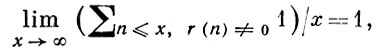
или, наконец, для r(n) имеется асимптотич. формула. Наименьшее число k, удовлетворяющее одному из перечисленных условий, обозначается соответственно g(A), G(A), G₀ (A), k₀ (А). В случае {а_i} = {р}, где {р} - последовательность простых чисел, при k = 3 получается теорема Виноградова: всякое достаточно большое нечетное число может быть представлено в виде суммы трех простых чисел; при k = 2 - теорема Чудакова: почти все четные числа могут быть представлены в виде суммы двух простых чисел.

Нек-рые задачи А. т. ч. решаются при помощи исследования структуры множеств, получающихся в результате суммирования последовательностей A_i {а_i}, заданных лишь их плотностями d(A_i) = inf_n A_i (n)/n, где А_i (n) = ∑_{1 ≤ αi ≤ n} 1. Из положительности d(A_i) при А₁ = A₂ =... = A_k = A уже следует, что g(A) < ∞. Применение этого факта к задачам А. т. ч., в к-рых суммируются последовательности нулевой плотности, осуществляется путем конструирования из данных последовательностей новых последовательностей с положительной плотностью. Ведущую роль при этом играют решета методы, с помощью к-рых доказывается положительность d(A_i). Таким способом Л. Г. Шнирельманом доказана теорема о представимости натуральных чисел в виде суммы ограниченного числа простых слагаемых, Ю. В. Линником найдено элементарное решение проблемы Варинга.

Элементарные методы решета, принадлежащие В. Бруну (см. Бруна решето) и А. Сельбергу (см. Сельберга решето), приводят в ряде задач А. т. ч. к результатам, недоступным пока современным аналитич. средствам. Однако наиболее законченные решения нек-рых задач А. т. ч. получаются путем комбинирования аналитических и элементарных методов. В методах решета принцип высеивания простых чисел из натурального ряда (см. Эратосфена решето) распространяется на совокупности последовательностей. Так, одновременное высеивание с должной точностью из последовательностей {m} и {2n - m} простых чисел, ≤ n^θ₁ и, соответственно, ≤ n^θ₂ (где θ₁ < 1 и θ₂ < 1 - надлежащим образом выбранные положительные константы), приводит к решению так наз. квазипроблемы Гольдбаха-Эйлера о представлении четного числа суммой двух чисел, одно из к-рых имеет не более k₁, а другое - не более k₂ простых множителей.

В 1959 Ю. В. Линником при помощи созданного им дисперсионного метода была решена проблема Харди-Литлвуда, а именно, было доказано (см. [2]), что всякое достаточно большое натуральное число может быть представлено в виде суммы простого числа и двух квадратов целых чисел. Дисперсионным методом был решен ряд так наз. бинарных проблем, связанных с нахождением числа Q(n) решений уравнения α + β = n, где α и β пробегают заданные последовательности чисел, достаточно хорошо распределенные в арифметич. прогрессиях. Для метода Линника характерно использование элементарных теоретико-вероятностных понятий, примененных П. Л. Чебышевым в его выводе закона больших чисел. С этой целью данное бинарное уравнение сводится к большому числу вспомогательных уравнений, для к-рых сопоставляются ожидаемые (S_i (n)) и истинные (Q_i (n)) количества решений уравнений. Если подсчет дисперсии показывает, что Q_i (n) «в среднем» мало отличаются от S_i (n), то Q(n) = ∑ S_i (n) (с допустимой погрешностью). Дисперсионный метод был использован также для исследования общего уравнения Харди-Литлвуда.

Область применения дисперсионного метода пересекается с областью применения метода большого решета, разработанного Ю. В. Линником в 1941. Этот метод позволяет высеивать последовательности при помощи простых чисел с возрастающим числом выбрасываемых вычетов. Фактически метод большого решета является следствием законов распределения слабо зависимых случайных величин.

В А. т. ч. существуют задачи, систематич. изучение к-рых относится к другим разделам теории чисел: проблема представимости целых чисел квадратичными формами и формами высших степеней; исследование диофантовых уравнений, допускающих трактовку с позиций общей А. т. ч.

В современной теории чисел интенсивно развиваются различные направления А. т. ч., наблюдается тенденция к перенесению проблем и методов А. т. ч. на произвольные поля алгебраич. чисел.

Лит. : [1] Виноградов И. М., Избранные труды, М., 1952; [2] Линник Ю. В., Дисперсионный метод в бинарных аддитивных задачах, Л., 1961; [3] Хуа Ло-ген, Метод тригонометрических сумм и его применения в теории чисел, пер. с нем., М., 1964; [4] Оstmann H. H., Additive Zahlentheorie, Bd 1-2, В., 1956; [5] Чудаков Н. Г., «Успехи матем. наук», 1938, вып. 4, с. 14-33; [6] Бредихин Б. М., там же, 1965, т. 20, в. 2 (122), с. 89-130.

Б. М. Бредихин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.