АДДИТИВНАЯ ТЕОРИЯ ИДЕАЛОВ

Расстановка ударений: АДДИТИ`ВНАЯ ТЕО`РИЯ ИДЕА`ЛОВ

АДДИТИВНАЯ ТЕОРИЯ ИДЕАЛОВ - одна из ветвей современной алгебры. Главная задача А. т. и. - представление любого идеала кольца (или другой алгебраич. системы) в виде пересечения конечного числа идеалов специального вида (примарных, терциарных, примальных, одночастных и др.). При этом вид представлений выбирается так, что: 1) для любого идеала существует нужное представление, или, что то же, справедлива нек-рая теорема «существования»; 2) выбранные представления должны быть единственны с точностью до каких-то ограничений, или, что то же, выполняется нек-рая теорема «единственности». Начало А. т. и. было положено в 20-30-х гг. 20 в. работами Э. Нётер [1] и B. Крулля [2].

Все особенности А. т. и. отчетливо проявляются в случае колец. Пусть R - нётерово кольцо, т. е. - ассоциативное кольцо с условием максимальности для идеалов. Если А-идеал в R, то существует наибольший идеал N кольца R, обладающий свойством: N^k ⊆ A для нек-рого натурального k ≥ 1. Этот идеал N наз. примарным радикалом идеала А (в кольце R) и обозначается через рr(A). Идеал Q кольца R наз. примерным, если для любых двух идеалов А, В в R выполняется условие:

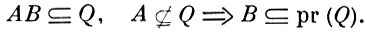
Для примарных идеалов верна теорема пересечения: пересечение любых двух примарных идеалов с одним и тем же примарным радикалом Р само есть примерный идеал с тем же радикалом Р. С помощью этой теоремы доказывается теорема существования: если кольцо R коммутативно, то для любого идеала A ≠ R существует такое представление идеала А в виде пересечения конечного числа примарных идеалов A_i :

А = А₁ ∩... ∩ А_n, (1)

что ни один из идеалов A_i не содержит пересечения остальных, и примарные радикалы рr(A_i) попарно различны. Такие представления наз. несократимыми, или примарно редуцированными (см. [1], [4]). Для этих представлений верна теорема единственности: если (1) и

А = B₁ ∩... ∩ B_m (2)

- два примарно редуцированных представления идеала А кольца R, то m = n и рr(A_i) = рr(B_i) для 1 ≤ i ≤ n, при надлежащей перенумеровке идеалов B_i .

Именно А. т. и. нётеровых коммутативных колец (классич. А. т. и.) нашла многочисленные применения в различных разделах математики.

Если кольцо R некоммутативно, то теорема «существования», указанная выше, перестает быть верной, в то время как теоремы «единственности» и «пересечения» верны. Этот факт начиная с 30-х гг. 20 в. привел к поискам такого обобщения классич. примарности на некоммутативный случай, при к-ром оставалась бы справедливой и теорема «существования». Было найдено нужное обобщение (см. [4]) - терциарность (см. Терциарный идеал). В дальнейшем было показано, что при нек-рых естественных ограничениях терциарность является единственным «хорошим» обобщением понятия примарности (см. [6], [7], [8]).

В 60-е гг. 20 в. А. т. и. развивалась в рамках теорий решеток, систем с частными и мультипликативных систем (см. [4], [5], [6]), что дало толчок развитию, напр., А. т. и. неассоциативных колец, нормальных делителей группы и подмодулей модуля.

Лит. : [1] Noether Е., «Math. Ann. », 1921, Bd 83, Н. 1-2, S. 24-66; [2] Krull W., там же, 1929, Bd 101, H. 4, S. 729-744; [3] 3арисский О., Самюэль П., Коммутативная алгебра, пер. с англ., т. 1, М., 1963; [4] Lеsiеur L., Сrоisоt R., Algèbre noethérienne non commutative, P., 1963; [5] Murata K., «J. Inst. Pol. Osaka City Univ. », 1959, v. A10, № 2, p. 91-115; [6] Андpунакиeвич В. А., Рябухин Ю. М., «Изв. АН СССР. Серия матем. », 1967, т. 31, № 5, с. 1057-90; [7] Rilеу J. A., «Trans. Amer. Math. Soc. », 1962, v. 105, №2, p. 177-201; [8] Гоян И. М., Pябухин Ю. М., «Матем. исследования», 1967, т. 2, в. 1, с. 14-25; [9] Fuсhs L., «Рrос. Amer. Math. Soc. », 1950, v. 1, № 1, p. 1-6; [10] Итоги науки. Алгебра. Топология. Геометрия. 1965, М., 1967, с. 133-180.

В. А. Андрунакиевич.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.