АДАМСА МЕТОД

Расстановка ударений: А`ДАМСА МЕ`ТОД

АДАМСА МЕТОД - конечно разностный метод решения задачи Коши для систем дифференциальных уравнений 1-го порядка

y' = f(x, y), y(х₀) = y₀ .

При интегрировании по сетке с постоянным шагом x_n = x₀ + nh расчетные формулы имеют вид:

а) экстраполяционные

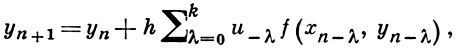
б) интерполяционные

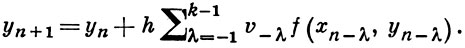
При одном и том же k формула б) точнее, но требует решения нелинейной системы уравнений для нахождения значения у_{n + 1} .

На практике находят приближение из а), а затем приводят одно-два уточнения по формуле

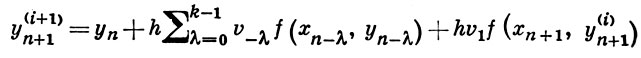
уточнения сходятся при условии h|v₁ | ||(∂f/∂y)|| < 1. Начальные условия y₁, ..., y_k для А. м., необходимые для начала вычислений по формулам а), определяются каким-либо специальным образом. Погрешность решения записывается в виде

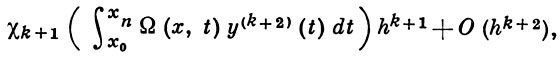
где Ω (х, t) - решение системы

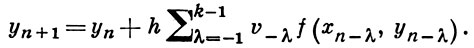
Структура члена O(h^{k + 2}) такова, что обычно при малых h он равномерно мал по сравнению с главным членом на больших промежутках интегрирования. Это обстоятельство обеспечивает возможность применения А. м. на больших промежутках интегрирования в случае абсолютно устойчивого решения дифференциальной задачи; в частности, в отличие от Милна метода, его можно применять для отыскания устойчивых периодич. решений дифференциальных уравнений. Стандартная программа А. м. интегрирования с автоматич. выбором шага существенно сложнее стандартной программы Рунге-Кутта метода, вследствие более сложного алгоритма при изменении шага и нестандартного выбора начальных значений y_k .

Для случая уравнений у' = - ау, а > 0, расчетная формула а) имеет вид:

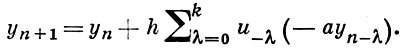
Это уравнение имеет частные решения у_n = Сμⁿ, где μ - корень уравнения

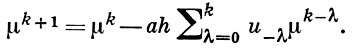
Если 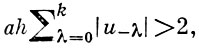то среди корней этого уравнения есть корень |μ | > 1, и ошибки округления сильно возрастают. При интегрировании с автоматич. выбором шага в ряде случаев это обстоятельство вызывает неоправданное измельчение шага. Однако в большинстве случаев А. м. оказывается несколько более экономичным по сравнению с методом Рунге - Кутта. А. м. предложен впервые Дж. К. Адамсом (J. С. Adams, 1855).

Лит. : [1] Березин И. С, Жидков Н. П., Методы вычислений, 2 изд., т. 2, М., 1962; [2] Бахвалов Н. С, Численные методы, 2 изд., М., 1975; [3] Тихонов А. Н., Горбунов А. Д., «Ж. вычисл. матем. и матем. физ. », 1962, т. 2, № 4, с. 537 - 48; [4] Лозинский С. М., «Изв. высш. учебн. заведений. Математика», 1958, № 5, с. 52 - 90; [5] Беленький В. 3., в сб. : Вычислительные методы и программирование, М., 1965, с. 253 - 61; [6] Бахвалов Н. С, «Докл. АН СССР», 1955, т. 104, № 5, с. 683 - 86.

Н. С. Бахвалов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.