АДАМАРА ТЕОРЕМА

Расстановка ударений: АДАМА`РА ТЕОРЕ`МА

АДАМАРА ТЕОРЕМА - 1) А. т. о лакунах (о пропусках): если номера n₁, n₂,... всех отличных от нуля коэффициентов степенного ряда

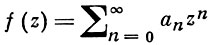
удовлетворяют условию

(*)

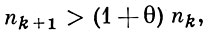
где θ > 0, то граница круга сходимости этого ряда является его естественной границей, т. е. функция не может быть аналитически продолжена за пределы этого круга. Условие (*) наз. условием Адамара; лакуны, удовлетворяющие условию Адамара, наз. лакунами Адамара. См. также Лакунарный ряд, Фабри теорема.

Лит. : [1] Hadamard J., «J. math, pures et appl. », ser. 4, 1892, t. 8, p. 101-86; [2]Бибербах Л., Аналитическое продолжение, пер. с нем., М., 1967.

Е. Д. Соломенцев.

2) А. т. о целых функциях - теорема о представлении целых функций с помощью их нулей, уточняющая Вейерштрасса теорему о бесконечных произведениях в случае целой функции f(z) конечного порядка ρ. Если, для простоты, f(0) ≠ 0, то

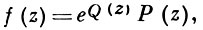
где Q(z) - многочлен степени не выше ρ, а

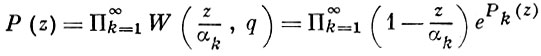
- каноническое произведение Вейерштрасса рода q ≤ р, построенное по нулям α_k функции f(z). Иначе говоря, А. т. утверждает, что род целой функции не превосходит ее порядка. Эта теорема использовалась Ж. Адамаром при доказательстве асимптотич. закона распределения простых чисел.

Лит. : [1] Hadamard J., «J. math, pures et appl. », ser. 4, 1893, t. 9, p. 171-215; [2] Mapкушeвич А. И., Теория аналитических функции, 2 изд., т. 2, М., 1968, гл. 2; [3] Левин Б. Я., Распределение корней целых функций, М., 1956.

Е. Д. Соломенцев.

3) А. т. об определителях: пусть D - определитель матрицы с элементами а_{μ ν}, μ, ν = 1, ..., n. Тогда имеет место неравенство

(*)

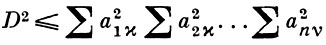
Равенство имеет место в том и только в том случае, когда

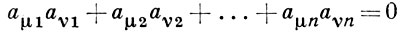
для каждой пары различных μ, ν, или когда хотя бы один множитель в правой части (*) равен нулю. Геометрич. смысл этой теоремы заключается в том, что объем параллелепипеда в n-мерном пространстве не превышает произведения длин его ребер, исходящих из одной вершины, и что равенство имеет место, когда эти ребра взаимно перпендикулярны или когда длина одного из ребер равна нулю.

Ж. Адамар в [1] рассматривал эту задачу для определителя с комплексными элементами.

Лит. : [1] Hadamard J., «Bull. sci. math. », 1893, ser. 2, t. 17, pt. 1, p. 240-6.

О. А. Иванова.

4) А. т. о трех кругах: если f(z) - голоморфная функция комплексного переменного r = r^eiφ в кольце 0 < r₁ < r₂ < ∞, непрерывная в замкнутом кольце r₁ ≤ r ≤ r₂, и М(r) = max |f(z)| при |z| = r, то справедливо неравенство

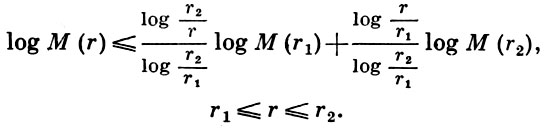
Это неравенство означает, что log М (r) есть выпуклая функция от log r. А. т. является частным случаем двух констант теоремы.

А. т. допускает обобщения в различных направлениях, в частности обобщение для других метрик, для гармония, и субгармонич. функций.

Лит. : [1] Hadamard J., «Bull. Soc. math. France», 1896, ser. 2, v. 24, p. 199-220; [2] Mapкушeвич А. И., Теория аналитических функций, 2 изд., т. 2, М., 1968, гл. 6; [3] Привалов И. И., Субгармонические функции, М. - Л., 1937, гл. 3; [4] Соломенцев Е. Д., «Докл. АН АрмССР», 1966, т. 42, М 5, с. 274-78.

Е. Д. Соломенцев.

5) А. т. мультипликационная, А. т. об умножении особенностей: если степенные ряды

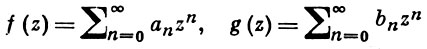
(1)

имеют, соответственно, радиусы сходимости r₁ > 0 и r₂ > 0, если S₁ и S₂ - звезды Миттаг-Леффлера (см. Звезда элемента функции), соответственно, для f(z) и g(z), и если α - множество особых точек функции f(z) на границе звезды S₁, а β - множество особых точек функции g(z) на границе звезды S₂, то степенной ряд

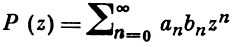
(2)

имеет радиус сходимости r ≥ r₁ r₂, а его звезда Миттаг-Леффлера S содержит звезду-произведение С(СS₁ × CS₂), где СА обозначает дополнение множества А и А × В - множество всех произведений pq чисел р ∈ А, q ∈ B; кроме того, из угловых и хорошо достижимых точек границы звезды-произведения особыми точками функции Р (z) могут быть лишь точки произведения множеств α × β. Первоначальные формулировки теоремы (см. [1], [2]) были несколько отличны от приведенной выше, они потребовали уточнений (см. [2]).

Степенной ряд (2) наз. адамаровскпм произведением, или адамаровской композицией, степенных рядов (1). Свойства адамаровского произведения, выявленные этой А. т. и в последующих исследованиях (см. [3]), позволяют использовать его в вопросах аналитич. продолжения степенных рядов, когда по коэффициентам ряда вида (2) оказывается возможным сделать нек-рые заключения об особенностях представляемой им аналитич. функции.

Если K - произвольное компактное множество, расположенное внутри звезды-произведения С(СS₁ × CS₂), то найдется такой замкнутый спрямляемый контур L, расположенный внутри С(СS₁ × CS₂) и охватывающий К, что для всех z ∈ K справедливо интегральное представление адамаровского произведения:

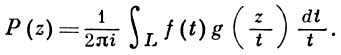
(3)

Представление (3) также применяется в вопросах аналитич. продолжения.

Лит. : [1] Hadamard J., «Acta math. », 1899, Bd 22, S. 55-63; [2] его жe, «Scientia Phys.-math. », 1901, №12; [3] Бибepбax Л., Аналитическое продолжение, пер. с нем., М., 1967.

Е. Д. Соломенцев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.