АДАМАРА ВАРИАЦИОННАЯ ФОРМУЛА

Расстановка ударений: АДАМА`РА ВАРИАЦИО`ННАЯ ФО`РМУЛА

АДАМАРА ВАРИАЦИОННАЯ ФОРМУЛА - формула

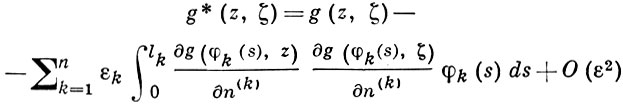
для Грина функции g(z, ζ) n-связной области G (n = 1, 2,...) комплексной z-плоскости. А. в. ф. имеет место, если: 1) граничные компоненты Г_k = {z : z = φ_k (s)} области G суть дважды дифференцируемые замкнутые кривые Жордана, s - длина дуги на Г_k, 0 ≤ s ≤ l_k ; 2) числа ε_k, ε_k > 0, настолько малы, что лежащие в G концы отрезков внутренних нормалей n^(k) к Г_k длины ε_k φ_k (s) образуют непрерывно дифференцируемые кривые, ограничивающие n-связную область G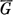^*, ^* ⊂ G; 3) ζ есть фиксированная точка в G^* . А. в. ф. представляет функцию Грина g^* (z, ζ) области G^* через g(z, ζ) с равномерной оценкой О(ε²), ε = mах ε_k, 0 ≤ k ≤ n, остаточного члена в прямом произведении области G^* и любого компакта из G. А. в. ф. применима и для функции Грина конечной римановой поверхности с краем.

Предложена Ж. Адамаром [1].

Лит. : [1] Нadamаrd J., «Мém. présentés par divers savants à l'Acad. sci. », 1908, t. 33; [2] Шиффep M., Спенсер Д. К., Функционалы на конечных римановых поверхностях, пер. с англ., М., 195-7, гл. 7.

И. А. Александров.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.