АВТОРЕГРЕССИОННЫЙ ПРОЦЕСС

Расстановка ударений: АВТОРЕГРЕССИО`ННЫЙ ПРОЦЕ`СС

АВТОРЕГРЕССИОННЫЙ ПРОЦЕСС - случайный процесс {X_t}, значения к-рого удовлетворяют при нек-рых постоянных a₁, ..., a_p уравнению авторегрессии

(*)

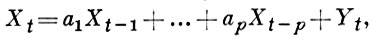
где р - нек-рое положительное число, а величины Y_t обычно предполагаются некоррелированными и одинаково распределенными со средним 0 и дисперсией σ² . Если все нули функции φ (z) = z^p - а₁ z^{p - 1} -... - а_p комплексного аргумента z лежат внутри единичного круга, уравнение (*) имеет решение

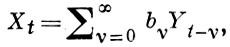
где b_v связаны с a_j соотношением

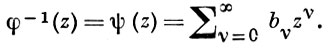
Пусть, напр., {Y_t} является процессом белого шума cо спектральной плотностью σ² /2π ; тогда единственным А. п., удовлетворяющим уравнению (*), будет стационарный в широком смысле процесс {X_t} со спектральной плотностью

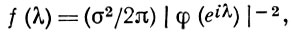
если φ (е^iλ) не имеет действительных нулей. Автоковариации процесса r_k = E X_t X_{t - k} удовлетворяют рекуррентному соотношению

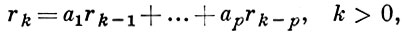
и в терминах b_v имеют вид

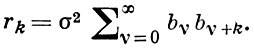
Параметры a_k авторегрессии связаны с коэффициентами автокорреляции процесса p_k = r_k /r₀ матричным соотношением

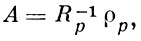
где А = {a₁, ..., a_p)', ρ_p = (ρ₁, ..., ρ_p) и R_p - матрица коэффициентов автокорреляции (уравнение Юна-Уокера).

Лит. : [1] Grenander U., Rosenblatt М., Statistical analysis of stationary time series, Stockh., 1956; [2] Xeннан Э., Анализ временных рядов, пер. с англ., М., 1964.

А. В. Прохоров.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.