АВТОНОМНАЯ СИСТЕМА

Расстановка ударений: АВТОНО`МНАЯ СИСТЕ`МА

АВТОНОМНАЯ СИСТЕМА обыкновенных дифференциальных уравнений - система обыкновенных дифференциальных уравнений, в к-рую не входит явно независимое переменное t (время). Общий вид А. с. 1-го порядка в нормальной форме:

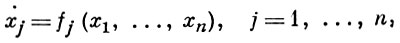
или, в векторной записи,

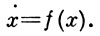
(1)

Неавтономная система 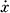= f(t, х) сводится к А. с, если ввести новую неизвестную функцию х_{n + 1} = t. Исторически А. с. возникли при описании физич. процессов с конечным числом степеней свободы. А. с. наз. также динамическими, или консервативными (см. Динамическая система).

Комплексная А. с. вида (1) эквивалентна вещественной А. с. с 2n неизвестными функциями

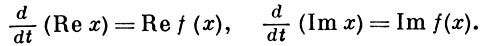
Содержательная теория комплексных А. с, отличная от вещественного случая, имеет место в случае аналитических f(x) (см. Аналитическая теория дифференциальных уравнений).

Будем рассматривать А. с. с действительными коэффициентами и их действительные решения. Пусть х = φ (t) - (произвольное) решение А. с. (1), Δ = (t_, t₊) - интервал его определения, x(t; t₀, х⁰) - решение с начальными данными х|_{t = t0} = х⁰ . Пусть G - область в ℝⁿ и f ∈ C¹ (G). Точка x⁰ ∈ G наз. положением равновесия (точкой покоя) А. с. (1), если f(х⁰) = 0. Положению равновесия отвечает решение φ (t) = x⁰, t ∈ ℝ = (- ∞, + ∞).

Локальные свойства решений.

1) Если φ (t) - решение, то φ (t + с) - решение при любом c ∈ ℝ.

2) Существование: при любых t₀ ∈ ℝ, x⁰ ∈ G решение x(t; t₀, х⁰) существует на нек-ром интервале Δ ∋ t.

3) Гладкость: если f ∈ C^p (G), р ≥ 1, то φ (t) ∈ C^{p + 1} (Δ).

4) Зависимость от параметров: пусть f = f(x, α), α ∈ G_α ∈ ℝ^m (G_α - область); если f ∈ C^p (G × G_α), р ≥ 1, то x(t; t₀, х⁰, α) ∈ С^p (Δ × Gα) (подробнее см. [1]-[4]).

5) Пусть х⁰ не является положением равновесия, тогда существуют окрестности V, W точек х⁰, f(x⁰), соответственно, и диффеоморфизм y = h(x) : V → W такие, что А. с. имеет вид 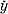= const в W.

Замена переменных х = φ (y) в А. с. (1) приводит к системе

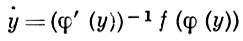
(2)

(φ '(y) - Якоби матрица).

Глобальные свойства решений.

1) Любое решение x = φ (t) А. с. (1) можно продолжить на интервал Δ = (t_, t₊). Если Δ = ℝ, то решение наз. неограниченно продолжаемым; если t₊ = + ∞, t_ > - ∞, то решение наз. неограниченно продолжаемым «вперед по времени» (аналогично - «назад»). Если t₊ < + ∞, то для любого компакта K ⊂ Ω, х⁰ ∈ К, существует τ = τ (K)<< t>₊ такое, что точка x(t; t₀, x⁰) находится вне К при t > τ (K) (аналогично при t_ > - ∞ ; см. Продолжаемость решений дифференциальных уравнений).

2) Продолжение единственно в том смысле, что любые два решения с общими начальными данными совпадают на общей области их определения.

3) Всякое решение А. с. принадлежит к одному из трех типов: а) непериодическое, причем φ (t₁) ≠ φ (t₂) для любых t₁ ≠ t₂, t_j ∈ ℝ ; b) периодическое, непостоянное; с) φ (t) = const.

Геометрическая интерпретация А. с. Каждому решению x = φ (t) ставится в соответствие кривая Г: x = φ (t), t ∈ Δ, лежащая в области G. Тогда G наз. фазовым пространством А. с., Г-фазовой траекторией, решение интерпретируется как движение по фазовой траектории. Фазовым потоком наз. отображение g^t : G → G по формуле g^t x⁰ = x(t; 0, х⁰) (т. е. каждая точка сдвигается за время t вдоль фазовой траектории). На своей области определения фазовый поток удовлетворяет условиям: 1) g^t x непрерывно по (t, х), 2) справедливо групповое свойство: g^{t₁ + t₂} x = g^t₁ g^t₂ x.

Имеет место теорема Лиувилля: пусть D ⊂ G - область с конечным объемом, v_t - объем области g₁ D ⊂ G; тогда

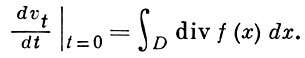
(3)

Для гамильтоновой системы из (3) следует сохранение фазового объема фазовым потоком. Другой вариант равенства (3): пусть x = φ (t, α) - семейство решений А. с. (1), α = (α₁, ..., α_{n - 1}) ∈ G_α - область, φ ∈ С¹ (Δ × G_α); тогда

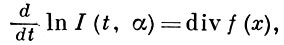
(3')

где I(t, α) = det ∂x/∂(t, α).

Структура фазовых траекторий.

1) Любые две фазовые траектории либо не имеют общих точек, либо совпадают.

2) Всякая фазовая траектория принадлежит к одному из типов: а) гладкая простая незамкнутая жорданова дуга, b) цикл, т. е. кривая, диффеоморфная окружности, с) точка (положение равновесия). Локальная структура фазовых траекторий в малой окрестности точки, отличной от положения равновесия, тривиальна (см. локальное свойство 5) решений): семейство фазовых траекторий диффеоморфно семейству параллельных прямых. Для линейной А. с. структура фазовых траекторий в окрестности положения равновесия известна, так как А. с. интегрируема (см. [5]). Для нелинейных А. с. этот вопрос принадлежит к числу не решенных до конца проблем даже при n = 2 (см. Качественная теория дифференциальных уравнений). Одним из аспектов этой проблемы является вопрос об устойчивости положения равновесия (см. Устойчивости теория). Ниже приведены нек-рые результаты. Пусть х⁰, у⁰ - положения равновесия систем (1) и

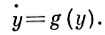
(1')

U, V - окрестности точек х⁰, у⁰ . Системы (1) и (1') наз. эквивалентными в окрестности положения равновесия х⁰, у⁰, если существуют U, V и взаимно однозначное отображение h : U → V такие, что (h ○ f^t)x = (g^t ○ h)x (если x ∈ U, f^t ∈ U, (g^t ○ h)x ∈ V), т. е. при замене y = h{x) траектории А. с. (1) переходят в траектории А. с. (1'). Эквивалентность наз. дифференцируемой (топологической), если h есть диффеоморфизм (гомеоморфизм). Пусть х⁰ - положение равновесия А. с. (1), матрица f'(x⁰) невырождена и не имеет чисто мнимых собственных значений. Тогда А. с. (1) в окрестности х⁰ топологически эквивалентна своей линейной части 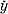= f'(x⁰)y. Полярный пример: А. с. 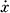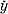= Ах, = Ву, где А, В - постоянные матрицы с чисто мнимыми собственными значениями и n < 2; неизвестно, когда эти А. с. топологически эквивалентны. Одной из самых фундаментальных задач теории А. с. является задача о структуре всего семейства фазовых траекторий. Наиболее полные результаты получены при n = 2, но даже в этом случае задача далека от своего разрешения.

Лит. : [1] Петровский И. Г., Лекции по теории обыкновенных дифференциальных уравнений, 6 изд., М. 1970; [2] Понтрягин Л. С., Обыкновенные дифференциальные уравнения, 2 изд., М.,. 1965; [3] Коддингтон Э. А. Левинсон Н., Теория обыкновенных дифференциальных уравнений, пер. с англ., М., 1958; [4] Арнольд В. И. Обыкновенные дифференциальные уравнения, М., 1971; [5] Немыцкий В. В., Степанов В. В., Качественная теория дифференциальных уравнений, 2 изд., М. - Л., 1949.

М. В. Федорюк.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.