АВТОМОРФНАЯ ФУНКЦИЯ

Расстановка ударений: АВТОМО`РФНАЯ ФУ`НКЦИЯ

АВТОМОРФНАЯ ФУНКЦИЯ - мероморфная функция нескольких комплексных переменных, инвариантная относительно некоторой дискретной группы Г аналитич. преобразований данного комплексного многообразия М:

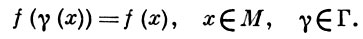
Часто под А. ф. понимают лишь функции, определенные в ограниченной связной области D n-мерного комплексного пространства Сⁿ, инвариантные относительно дискретной группы Г автоморфизмов этой области.

Факторпространство Х = М/Г может быть наделено комплексной структурой и А. ф. суть мероморфные функции на X. Подавляющее большинство изученных случаев относится к ситуации, когда пространство X имеет компактификацию X¯. В определение А. ф. естественно включается тогда требование ее продолжимости на все пространство X в виде мероморфной функции. Если M = D (т. е. ограниченная связная область), то это условие необходимо требовать лишь при n = 1 (если n > 1 или М/Г компактно, условие выполняется автоматически). Легко проверяется, что А. ф. образуют поле K(Г), изучение к-рого составляет одну из основных задач теории А. ф.

Наиболее подробно исследованы А. ф. одного переменного. Основы их теории заложены в 19 в. Ф. Клейном (F. Klein [1]) и А. Пуанкаре (Н. Poincare [2]). В качестве многообразия М здесь обычно рассматривают односвязную область. Различаются три случая: М = P¹ (С) (комплексная проективная прямая, или сфера Римана), М = С и М = Н (верхняя полуплоскость {z ∈ C : Im z > 0}). В первом случае дискретные группы Г конечны, кривые М/Г суть алгебраич. кривые рода О (см. Род кривой) и, следовательно, А. ф. образуют поле рациональных функций. Примерами А. ф. в случае М = С служат периодич. функции (так, функция e^{2π iz} инвариантна относительно группы сдвигов {z → z + n, n ∈ z}) и, в частности, эллиптич. функции. Для последних кривая М/Г компактна и является эллиптич. кривой. Поле K(Г) в этом случае будет полем всех алгебраич. функций на М/Г. Наконец, для М = Н и дискретных групп Г таких, что Н/Г компактно или имеет конечный объем (в метрике Пуанкаре), H/Г - алгебраич. кривая, а K(Г) - также поле всех алгебраич. функций на М/Г. Род g этой кривой можно определить, построив для группы Г фундаментальную область в виде многоугольника на верхней полуплоскости Н (рассматриваемой как плоскость Лобачевского). Основной способ построения А. ф. в этой ситуации состоит в рассмотрении отношения двух автоморфных форм одинакового достаточно большого веса. Этот способ принадлежит А. Пуанкаре, к-рый доказал с его помощью приведенные выше результаты о строении полей А. ф. (см. [2], [3], [4]). Аналогом этой конструкции для эллиптич. функций является представление их в виде отношения тета-функций. С помощью теории униформизации можно показать, что таким образом получаются все поля алгебраич. функций от одной переменной [3].

Эти результаты, полученные еще в 19 в., дают полное описание полей А. ф. для n = 1 и таких групп Г, что пространство Н/Г имеет конечный объем. Случай групп Г с бесконечным объемом пространства Н/Г (клейновы группы) гораздо сложнее и интенсивно изучается вплоть до настоящего времени (см. [5], [6]).

В 20 в. основное внимание в теории А. ф. уделяется функциям нескольких переменных. Пожалуй, единственным примером А. ф. от n переменных, детально изученным в 19 в., являются абелевы функции, связанные с абелевыми многообразиями подобно тому, как связаны эллиптич. функции с эллиптич. кривыми [1], [7]. Первым примером А. ф. n переменных в ограниченной области D явились модулярные функции Зигеля [7] (см. Модулярная группа). Их область определения представляет собой n-мерное обобщение верхней полуплоскости Н и является одним из основных примеров ограниченной симметрич. области. К. Зигелю (С. Siegel) принадлежат также первые общие результаты о произвольных А. ф. в ограниченной области D. Обобщая упомянутую выше конструкцию Пуанкаре построения А. ф., он показал, что в поле K(Г) всегда существует по крайней мере n алгебраически независимых функций.

В дальнейшем основные усилия были направлены на выяснение, для каких областей D и групп Г выполняется следующее утверждение, получившее название теоремы об алгебраических соотношениях. Если f₁, ..., f_n - алгебраически независимые функции, то поле K(Г) есть конечное алгебраич. расширение поля рациональных функций С(f₁, ..., f_n) ⊂ K(Г).

Теорема эта доказана к настоящему времени (1977) в следующих случаях: 1) если факторпространство D/Г компактно [7]; 2) если группа Г псевдовогнута [8]; 3) если D - симметрическая область, а Г - арифметическая группа. Псевдовогнутая группа определяется следующим образом. Пусть X - подобласть области D, содержащаяся в ней вместе с замыканием. Тогда точка границы х₀ ∈ ∂Х наз. псевдовогнутой, если для любой открытой окрестности U точки х₀ и для любой регулярной в U функции φ (х) существует точка x ∈ U ∩ X такая, что |φ (х)| ≥ |φ (х₀)| - Группа Г наз. псевдовогнутой, если существует подобласть X ⊂ D такая, что каждая граничная точка х ∈ ∂Х переводится преобразованием из Г либо во внутреннюю точку, принадлежащую X, либо в псевдовогнутую точку границы ∂Х.

Вопрос о природе и свойствах алгебраич. многообразий, возникающих в теории А. ф. n переменных, в отличие от случая одной переменной, исследован мало.

Важные обобщения понятия А. ф.-автоморфные формы, тета-функции и нек-рые др. Все они - частные случаи следующей общей конструкции. Рассматривается расслоение L на М и действие на нем группы Г. Тогда можно определить сечения расслоения L, инвариантные относительно Г. А. ф. получаются, когда расслоение L и действие группы Г тривиальны.

При изучении А. ф. выявилась важная роль группы автоморфизмов области D. Именно на этом пути понятия и методы теории А. ф. были перенесены в теорию алгебраических групп, где они играют существенную роль при описании бесконечномерных представлений (см. [10]).

С самого начала своего развития теория А. ф. была богата связями с другими разделами математики. Прежде всего сюда относится алгебраич. геометрия. Помимо упомянутых выше результатов, методы А. ф. важны для исследования многообразий модулей таких объектов, как алгебраич. кривые и абелевы многообразия. Существенное значение имеют А. ф. и для теории чисел. В настоящее время они служат единственным инструментом для изучения дзета-функций алгебраич. многообразий (см. [11]). Другое весьма многообещающее теоретико-числовое направление в теории А. ф. - исследование р-адических А. ф. и автоморфных форм (см. [9]). Наконец, следует упомянуть о применении А. ф. при исследовании обыкновенных дифференциальных уравнений в комплексной области [12], или о построении решений алгебраич. уравнений выше 4-й степени посредством автоморфных функций.

Лит. : [1] Клейн Ф., Лекции о развитии математики в XIX столетии, пер. с нем., ч. 1, М. - Л., 1937, гл. 8; [2] Пуанкаре А., Избр. труды, т. 3, пер. с франц., М., 1974; [3] Форд Л. Р., Автоморфные функции, пер. с англ., М. - Л., 1936; [4] Бейтмен Г., Эрдейи А., Высшие трансцендентные функции. Эллиптические и автоморфные функции, функции Ламе и Матье, пер. с англ., М., 1967; [5] Адамар Ж., Неевклидова геометрия в теории автоморфных функций, пер. с франц., М., 1952; [6] Кра И., Автоморфные формы и клейновы группы, пер. с англ., М., 1975; [7] 3игель К. Л., Автоморфные функции нескольких комплексных переменных, пер. с англ., М., 1954; [8] Андреотти А., Грауерт Г., Алгебраические поля автоморфных функций, в кн. : Комплексные пространства, М., 1965; [9] Modular functions of one variable, v. 1-3, В., 1973; [10] Жаке Э., Ленглендс Р., Автоморфные формы на GL (2), пер. с англ., М., 1973; [11] Шимура Г., Введение в арифметическую теорию автоморфных функций, пер. с англ., М., 1973; [12] Голубев В. В., Лекции по аналитической теории дифференциальных уравнений, М., 1950.

А. Н. Андрианов, А. Н. Паршин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.