АВТОМАТОВ СПОСОБЫ ЗАДАНИЯ

Расстановка ударений: АВТОМА`ТОВ СПО`СОБЫ ЗАДА`НИЯ

АВТОМАТОВ СПОСОБЫ ЗАДАНИЯ - варианты описания автоматов, их функционирования или поведения. А. с. з. зависят от подхода к определению понятия автомата. При макроподходе (см. Автомат конечный) описывается внешнее поведение автомата; при микроподходе задание должно содержать описание элементов, из к-рых строится автомат, и схемы их соединения. Ниже приводятся способы задания конечных автоматов.

Макроподход. В этом случае задать конечный автомат 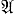= (A, S, В, φ, ψ) при условии, что заданы алфавиты А = {a₁, ..., a_m}, S = {s₁, ..., s_n}, В = {b₁, ..., b_k}, - значит описать функции φ и ψ или описать поведение этого автомата (см. Автомата поведение). Для задания функций φ и ψ обычно используют таблицу переходов, диаграмму переходов или матрицу переходов. 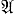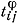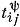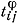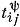Таблица переходов Т автомата состоит из двух подтаблиц T_φ = |||| и T_ψ = ||||, i = 1, ..., n, j = 1, ..., m, ∈ S, ∈ B. Функции φ и ψ определяются как φ (s_i, a_j) = 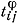, ψ (s_i, a_j) = 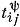. Если все столбцы T_ψ совпадают, то таблица Т задает автомат Мура. Напр., пусть A₀ = {а₁, а₂}, S₀ = {s₁, s₂}, B₀ = {b₁, b₂}; тогда таблица Т (рис. 1) задает функции φ₀ и ψ₀ нек-рого автомата ⁰ (на рис. 2 показаны подтаблицы T_φ и T_ψ таблицы Т).

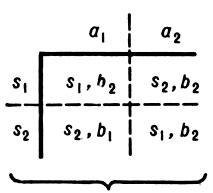
Рис. 1

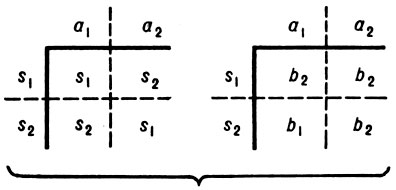
Рис. 2

Диаграмма автомата (диаграмма переходов автомата) - это ориентированный граф G, вершинам к-рого взаимно однозначно соответствуют элементы S, а ребрам приписаны нек-рые множества пар вида (а, b), а ∈ А, b ∈ В. Из каждой вершины G исходит по крайней мере одно ребро; при этом множество 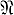всех пар, приписанных ребрам, исходящим из одной вершины, имеет вид = {(a₁, b_i1), (a₂, b_i2), ..., (a_m, b_im)}. Функции φ и ψ определяются следующим образом: φ (s_i, a_j = s_r, ψ (s_i, a_j) = b_p, если ребру, исходящему из вершины s_i, приписана пара a_i, b_p) и это ребро ведет в вершину s_r . Нек-рые свойства автоматов удобно формулировать на языке диаграмм (связность автомата, достижимость состояний и т. п.). На рис. 3 представлена диаграмма переходов автомата ⁰ .

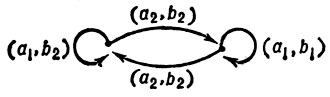
Рис. 3

Матрица переходов используется для описания функционирования переходной системы 〈 A, S, φ 〉 (см. Автомат конечный). Она представляет собой (n × n) - матрицу P = ||P_ij ||, элементами к-рой являются подмножества алфавита А (может быть, пустые) такие, что а ∈ Р_ij тогда и только тогда, когда φ (s_i, a) = s_j и, следовательно, для всякого i = 1, 2, ..., n имеет место P_ip ∩ P_ir = ∅ при р ≠ r и ∩ⁿ_{j = 1} P_ij = A. Чтобы распространить функцию φ на множество S × A^* (А^* - множество всех слов в алфавите А, включая пустое слово), рассматривают последовательность степеней матрицы Р. Умножение матрицы Р на себя производится по обычному алгоритму с использованием вместо операций умножения и сложения операций произведения (конкатенации) и объединения множеств слов. Если α ∈ А^* - слово длины d и α ∈ P_ij^(d) где P_ij^(d) - элемент матрицы P^d, то φ (s_i, α) = s_j . Так, матрица переходов Р переходной системы 〈 А₀, S₀, φ₀ 〉 и матрица Р² имеют, соответственно, вид:

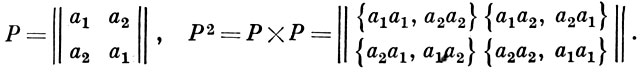
С указанными А. с. з. связан ряд алгоритмов минимизации (приведения) и синтеза автоматов.

Для задания поведения инициального (не обязательно конечного) автомата 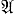_S1 (преобразователя) необходимо описать функцию f(α) = ψ (s₁, α), отображающую А^* в В^* (или А^∞ в В^∞, где A^∞, В^∞ - множества всех сверхслов в алфавитах А и В, соответственно). Эта функция может быть задана информационным деревом. Из каждой вершины информационного дерева исходит т ребер, взаимно однозначно соответствующих буквам алфавита А. Каждой вершине приписано состояние автомата 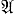_S1, а каждому ребру - буква алфавита В следующим образом. Корню приписано состояние s₁ . Если нек-рой вершине приписано состояние s_i, то ребру, соответствующему букве а из А, приписана буква b = ψ (s_i, а) и вершине, в к-рую ведет это ребро, приписано состояние s_j = φ (s_i, а). Каждому слову α = α₁ α₂ ...α_r ∈ А^* соответствует единственная последовательность ρ = ρ₁ ρ₂ ...ρ_r ребер этого дерева такая, что ρ₁ исходит из корня и ρ_{i + 1} исходит из вершины, в к-рую ведет ρ_i . Слово β = β₁ β₂ ...β_r, где β_i - буква из В, приписанная ребру ρ_i, i = 1, ..., r, совпадает со значением 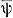(s₁, а). Если функция f реализуется конечным автоматом, то соответствующее информационное дерево может быть задано эффективно своим конечным поддеревом. На рис. 4 изображено поддерево информационного дерева, задающее поведение инициального автомата 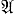⁰_S1 (левые ребра, исходящие из вершин, соответствуют символу a₁ правые - символу а₂).

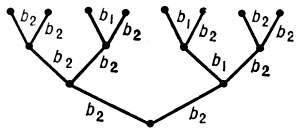
Рис. 4

Описание поведения конечного автомата (акцептора) в терминах представимого события (сверхсобытия) может быть сделано с помощью регулярного выражения (см. Регулярное событие). Такие события могут быть также заданы как множества слов, порождаемых (выводимых) в нек-рой формальной системе (полу-Туэ грамматике и т. п.). Система полу-Туэ в этом случае задается четверкой Т = (A, S, ξ, ω), где A, S - конечные алфавиты, A ∩ S = ∅, ξ - аксиом схема вида s₀ X и ω - множество схем правил вывода вида saX → s'X, r → r, где s, s', r ∈ S, а ∈ А и X - переменная, принимающая значения из А^* . При этом, если saX → s'X и saX → s''X принадлежат ω, то s' = s''. Слово α ∈ А^* выводимо в системе Т, если существует последовательность слов s₀ α = w₁, w₂, ..., w_n такая, что w_{i + 1} получается из w_i, i = 1, ..., n - 1, применением нек-рого правила из ω, w_n ∈ S и ω не содержит правила w_n → w_n . Аналогичный вид имеет грамматика, порождающая регулярное событие. Она задается четверкой Г = (А, S, s₁, ω), где s₁ из S - аксиома, ω - множество правил вида s_i → as_j, либо s_i → а. Слово α = α₁ α₂ ...α_n выводимо в Г, если в ω имеются правила s₁ → α₁ s_i2, s_i2 → α₂ s_i3, ..., s_in → α_n . Известны алгоритмы, позволяющие получать матрицу переходов автомата по формальным системам описанного типа. Так, событие, представимое в акцепторе 〈 А₀, S₀, φ₀, s₁ 〉 состоянием s₂, может быть, напр., задано как множество слов, выводимых в системе полу-Туэ, к-рая имеет вид:

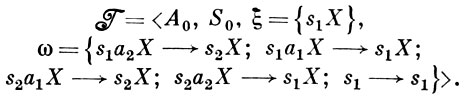
Существует ряд других А. с. з. Напр., переходная система 〈 А, S, φ 〉, не обязательно конечная, может быть задана как алгебра 〈 S, Ф&$62;, где Ф = {φ_a |а ∈ A} есть множество унарных операций на S таких, что φ_a (s) = φ (а, s). Так, переходную систему 〈 А₀, S₀, φ₀ 〉 можно рассматривать как алгебру 〈 S₀, {φ_a1, φ_a2} 〉, где φ_a1 (s₁) = s₁, φ_a1 (s₂) = s₂, φ_a2 (s₂) = s₁, φ_a1 (s₁) = s₁ . Можно также рассматривать алгебру 〈 S̃, Ф̃ 〉, где S̃ - множество слов вида sα, s ∈ S, α ∈ А^*, и Ф̃ = {φ ̃_a |a ∈ A} - множество унарных операций на S̃ таких, что φ̃_a (sa) = sα a. Алгебра 〈 S̃, Ф̃ 〉 задается системой образующих S и множеством определяющих соотношений ω = {s_i α_i = s'_i α '_i, i = 1, 2...}. Такая алгебра задает автомат (вообще говоря, частичный) 〈 A, S, φ 〉 такой, что если s_i α_i = s'_i α '_i - соотношение из ω, то φ (s_i α_i) = φ (s'_i α '_i). Напр., переходную систему 〈 A₀, S₀, φ₀ 〉 можно задать системой образующих S₀ и множеством определяющих соотношений ω = {s₁ = s₁ a₁, s₁ = s₂ a₂, s₂ = s₁ a₂, s₂ = s₂ a₁}. При этом предполагается, что φ (s₁, Λ) = s₁, φ (s₂, Λ) = s₂ .

Поведение автомата может быть описано средствами языка логики одноместных предикатов. При этом выбор класса формул, задающих конечные автоматы, осуществляется различными способами. Описание может быть неполным, тогда оно определяет нек-рый класс автоматов, поведение к-рых идентично с точностью до этого описания. Напр., «анкетный» подход связан с заданием класса автоматов с помощью фрагментов информационных деревьев, частичного определения функций φ и ω и т. п.

Указанные А. с. з. могут быть использованы с соответствующими модификациями при макроподходе к поведению нек-рых обобщений конечных автоматов (недетерминированных, бесконечных и т. п., см. Автомат). Так, элементами таблицы T_φ конечного недетерминированного автомата могут быть произвольные подмножества множества S. Поведение конечного недетерминированного акцептора описывается регулярным выражением, как и в детерминированном случае. Другими обобщениями конечных автоматов являются конечные автоматы вероятностные, автоматы над термами, мозаичные структуры и т. п.

Задать вероятностный автомат 〈 A, S, B, μ 〉, если известны алфавиты A = {a₁, ..., a_m}, В = {b₁, ..., b_k}, S = {s₁, ..., s_n), - значит при любых фиксированных i и j (l ≤ : i ≤ n, 1 ≤ j ≤ m) указать условную вероятностную меру μ_ij (s_r, b_q) нa множестве всех пар (s_r, b_q), r = 1, ..., n, q = 1, ..., к. Для этого обычно рассматривают систему квадратных матриц с неотрицательными элементами

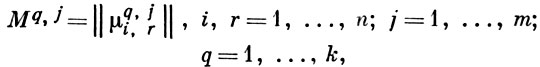
такую, что каждая матрица 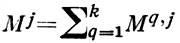является стохастической. Мера μ определяется так: μ_ij (s_r, b_q) = μ_{i, r}^{q, j} . Вероятностный автомат 〈 A, S, B, μ 〉 рассматривается совместно с нек-рым начальным распределением вероятностей на множестве S:

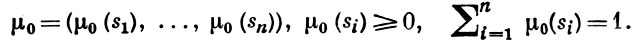
Иногда при задании вероятностных автоматов ограничиваются либо указанием матриц М^j, либо указанием матриц 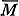^j = ||μ^j_{i, q} ||, где

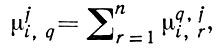
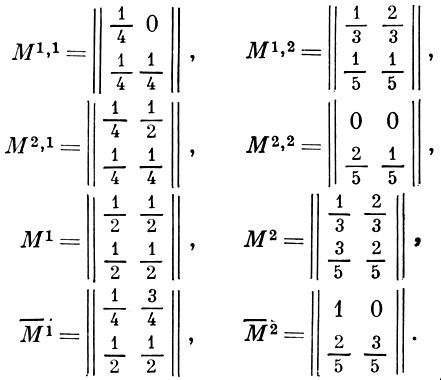
i = 1, ..., n, q = 1, ..., k, j = 1, ..., m. Любая конечная Маркова цепь может рассматриваться как конечный вероятностный автомат, у к-рого матрицы М^j, j = 1, ..., m, совпадают. Ниже представлены система матриц, задающая нек-рый вероятностный автомат 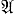(n = 2, k = 2, m = 2), и матрицы М¹, М², 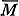¹, 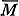² этого автомата:

Чтобы задать конечный автомат над термами 〈 A, S, σ, α_a 〉, когда известны алфавиты А = {a₁, ..., a_m}, S = {s₁, ..., s_n}, необходимо, во-первых, указать отображение σ множества А в конечное множество неотрицательных целых чисел, причем так, чтобы существовал хотя бы один элемент а ∈ А такой, что σ (a) = 0, а во-вторых, для всякого а_i ∈ A, i = 1, ..., m, требуется определить σ (a_i)-местную функцию α_ai, отображающую множество [S]^{σ (a_i)} = S ×... × S в S. Каждому элементу а ∈ А такому, что σ (а) = 0, ставится в соответствие элемент α_a ∈ S, наз. начальным состоянием автомата. Напр., если А = {а₁, а₂}, S = {s₁, s₂}, σ (а₁) = 0, σ (а₂) = 2, α_a1 = s₁, α_a2 (s₁, s₁) = s₂, α_a2 (s₁, s₂) = s₁, α_a2 (s₂, s₁) = s₂, α_a2 (s₂, s₂) = s₂, то функции σ, α_a1, α_a2 задают нек-рый автомат над термами (А, S, σ, {α_a1, α_a2}) с начальным состоянием s₁ .

Чтобы задать мозаичную структуру (бесконечное соединение переходных систем вида 〈 A, S, φ 〉, где А = S^r, см. Автомат), необходимо для каждой целочисленной точки n-мерного пространства определить конечное упорядоченное множество целочисленных точек - ее окрестность. При этом входной алфавит А переходной системы 〈 A, S, φ 〉, помещенной в нек-рую точку, есть декартово произведение множеств состояний переходных систем, помещенных в точки ее окрестности. Напр., пусть S = {s₁, s₂} и для всякой целочисленной точки двумерного пространства (α, β) ее окрестность D_{α, β} есть упорядоченное множество {(α - 1, β), (α, β + 1), (α + 1, β)} - Чтобы задать однородную двумерную мозаичную структуру, определяют функцию φ следующим образом: φ (s₁, s₁) = s₁, φ (s', s', s''') = s₂ в остальных случаях. Входной алфавит А в данном случае - декартово произведение S × S × S.

Микроподход. При микроподходе задать структурный автомат - значит описать элементы, из к-рых он построен, и схему их соединения. Описание может производиться на различных уровнях детализации. Часто ограничиваются рассмотрением так наз. канонической схемы построения автоматов; при этом элементы делят на две группы - функциональные элементы (автоматы с одним состоянием) и элементы памяти. Канонич. схема (рис. 5) состоит из двух функциональных блоков f и g с присоединенными к ним элементами памяти, в качестве к-рых используются автоматы Мура: 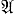_i = 〈 R_i, S_i, Q_i, φ_i, ψ_i 〉 i = 1, ..., l. Блоки f и g построены из функциональных элементов. При данном способе задания структуру этих блоков не описывают, а задают (напр., таблично) реализуемые ими вектор-функции:

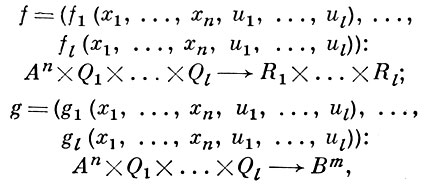
где Aⁿ и B^m -, соответственно, входной и выходной алфавиты канонич. схемы. Эта схема задает структурный автомат 〈 Аⁿ, S, В^m, φ, ψ 〉, где S = S₁ ×... × S_l, а функции φ и ψ определяются следующим образом:

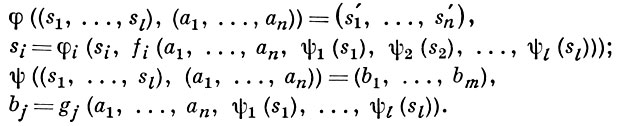
Важным примером структурных автоматов являются логич. сети (см. Автомат конечный). На рис. 6 представлена канонич. схема автомата 〈 А̃, S̃, В̃, φ̃, ψ̃ 〉, изоморфного автомату 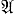⁰, диаграмма к-рого изображена на рис. 3, Ã = S̃ = B̃ = {0, 1}. Автомат 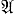' = 〈 S̃, S̃, S̃, φ ', ψ ' 〉 - автомат Мура такой, что φ '(1, z) = z, φ '(0, z) = z.

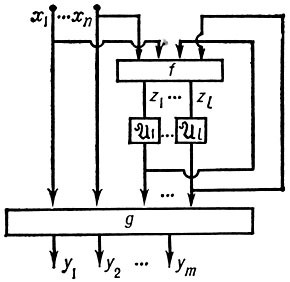
Рис. 5.

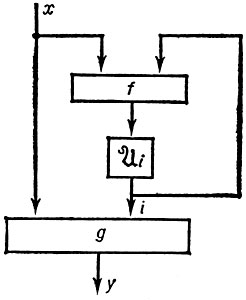
Рис. 6.

Для описания структурных автоматов часто используются канонические уравнения, т. е. системы вида:

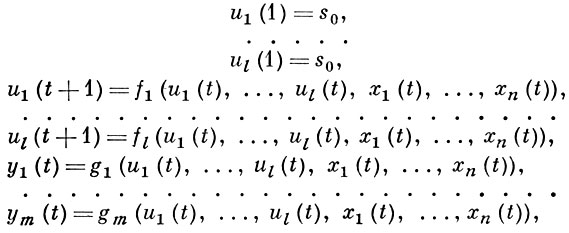
где t = 1, 2,... - целочисленный параметр, s₀ ∈ S, а функции f_i, i = 1, ..., l, g_i, i = 1, ..., m и переменные х_r, r = 1, ..., n, принимают значения из множества А. Этой системе соответствует канонич. схема, в к-рой все элементы памяти совпадают: 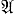_i = 〈 А, S, В, φ, ψ, s₀ 〉, где A = S = B, i = 1, ..., l; φ (a, a') = a', ψ (a, a') = a. Функционирование автомата 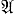_i содержательно может быть описано следующим образом. Пусть в момент времени t входу 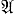_i приписана буква a(t), тогда эта же буква будет приписана выходу 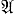_i в момент t + 1. На рис. 6 представлен автомат 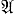, канонич. уравнения к-рого имеют вид:

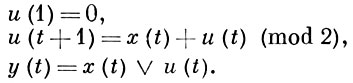
В общем случае описание структурных автоматов связано с заданием набора элементарных автоматов и нек-рого класса «правильно устроенных» схем (сетей), причем последние обычно определяются индуктивно.

Лит. : [1] Автоматы. Сб. статей, пер. с англ., М., 1956; [2] Глушков В. М., Синтез цифровых автоматов, М., 1962.

В. А. Буевич, С. В. Алешин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.