АВТОМАТОВ КОМПОЗИЦИИ

Расстановка ударений: АВТОМА`ТОВ КОМПОЗИ`ЦИИ

АВТОМАТОВ КОМПОЗИЦИИ - операции, позволяющие из одних автоматов получать другие, более сложные, путем соединения исходных автоматов по определенным правилам. А. к. играют важную роль в задачах синтеза и разложения автоматов. Важнейшими и наиболее употребительными А. к. являются прямое произведение, суперпозиция, обратная связь.

Прямым произведением автоматов 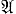_i = (A_i, S_i, В_i, φ_i, ψ_i), i = 1, ..., n, наз. автомат 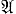= (A, S, В, φ, ψ), у к-рого

S = S₁ ×... × S_n, A = A₁ ×... × A_n, B = B₁ ×... × B_n

а функции φ (s, а) и ψ (s, а) определяются соотношениями:

φ ((s₁, ..., s_n), (a₁, ..., a_n)) = (φ₁ (s₁, a₁), ..., φ_n (s_n, a_n)), ψ ((s₁, ..., s_n), (a₁, ..., a_n)) = (ψ₁ (s₁, a₁), ..., ψ_n (s_n, a_n))

Под суперпозицией автоматов 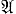₁ = (A₁, S₁, В₁, φ₁, ψ₁) и 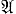₂ = (A₂, S₂, В₂, φ₂, ψ₂) понимают автомат 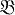= (A₁, S, В₂, φ, ψ). У к-рого S = S₂ × S₁ а

φ ((s₂, s₁), a) = (φ₂ (s₂, ψ₁ (s₁, a)), φ₁ (s₁, a))

и

ψ ((s₂, s₁), a) = ψ₂ (s₂, ψ₁ (s₁, a)),

В вопросах полноты и синтеза автоматов большую роль играет операция обратной связи. Эта операция применима к автоматам с n входами и m выходами: 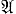= (A, S, В, φ, ψ), где A = A₁ ×... × A_n, B = B₁ ×... × B_m,

ψ (s, (a₁, ..., a_n)) = (ψ₁ (s, (a₁, ..., a_n)), ..., ψ_m (s, (a₁, ..., a_n)))

таким, что для нек-рых i, j имеет место B_i = A_j функция ψ_i не зависит от a_j, т. е.

ψ_i = ψ_i (s, (a₁, ..., a_{j - 1}, a_{j + 1}, ..., a_n))

Тогда в применении к i-му выходу и j-му входу автомата 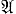операция обратной связи дает автомат 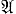' = (A', S, В, φ ', ψ ') такой, что A' = A₁ ×... × A_{j - 1} × A_{j + 1} ×... × A_n,

φ'(s, (a₁, ..., a_{j - 1}, a_{j + 1}, ..., a_n)) = φ (s, (a₁, ..., a_{j - 1}, ψ_i (a₁, ..., a_{j - 1}, a_{j + 1}, ..., a_n), a_{j + 1}, ..., a_n)),

ψ'(s, (a₁, ..., a_{j - 1}, a_{j + 1}, ..., a_n)) = ψ (s, (a₁, ..., a_{j - 1}, ψ_i (a₁, ..., a_{j - 1}, a_{j + 1}, ..., a_n), a_{j + 1}, ..., a_n)),

Кроме указанных, иногда используются другие виды А. к., напр. произведение, прямая сумма, полупрямое произведение и т. д.

Лит. : [1] Глушков В. М., «Успехи матем. наук», 1961, т. 16, в. 5 (101), с. 3-62; [2] Кудрявцев В. В., «Проблемы кибернетики», 1965, в. 13, с. 45 - 74.

В. Н. Редько.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.